
En este trabajo se explorarán las técnicas modernas de síntesis de imágenes físicamente realistas basadas en Path-Tracing en tiempo real. Para ello, se utilizarán métodos de integración de Monte Carlo con el fin de disminuir el tiempo de cómputo.
Se diseñará un software basado en la interfaz de programación de aplicaciones gráficas Vulkan, utilizando como soporte un entorno de desarrollo de Nvidia conocido como nvpro-samples (NVIDIA 2022b). El software implementará un motor gráfico basado en path tracing. Este motor será capaz de renderizar numerosas escenas, cambiar los parámetros del algoritmo path tracing y modificar las fuentes de iluminación en tiempo de ejecución.
Con el fin de explorar cómo afectan diferentes métodos al ruido final de la imagen, se estudiarán algunas técnicas de reducción de varianza como muestreo directo de fuentes de iluminación, muestreo por importancia, supersampling o acumulación temporal. Además, el motor desarrollado se comparará con una implementación del software creado en los libros de (Shirley 2020a) “Ray Tracing in One Weekend series”, la cual utiliza exclusivamente la CPU. Se comprobarán las diferencias entre ambas versiones, estudiando los puntos fuertes de cada una.
Palabras clave: raytracing, ray tracing, path tracing, métodos de Monte Carlo, integración de Monte Carlo, transporte de luz, iluminación global, Vulkan.
To be able to capture a moment. Every human civilization in record has always found a way to immortalise the idiosyncrasies of its sociecy. We are not immune to this phenomenon, so it is only natural we try to use the lastest technology to achieve the most faithful representation of our world. Computers have the ability to produce realistic images and astonishing simulations. Although there have been tremendous advances in the field, many of the techniques we use today are still based on the old days of computation, especially in 3D rendering.
Rasterization is one of those methods. It allows us to transform a virtual environment to a raster image, which is a set of pixels. It is an extremelly fast method given how it works, which is just a mapping of the scene geometry into a 2D plane. Its simplicity makes it a great quick way of rendering an image, but it comes at the expense of fidelity.
We can solve this issue with Ray tracing. Instead of projecting virtual geometry into a plane, this algorithm tries to simulate how light works by casting rays of light into the scene from the camera. These rays then intersect with objects and collect information about them. This has one key advantage over rasterization: it manages to us parts of the scene which were not visible to the camera.
Path tracing takes this idea to the next level: instead of stopping in the first intersection, it makes the rays bounce freely through the scene. These rays gather information about object materials, light sources and many more elements. Then, the algorithm computes the color of the pixel by considering how much light those rays have acummulated over their traversal. This manner of working results in an improvement over ray tracing, which is often called global illumination.
Global illumination is a physical phenomenon related to indirect lightning that occurs when photons bounce off of objects and are reflected back into a room. In rasterization, it has been traditionally faked by using methods such as ambient occlusion, light maps and so on, since it is crucial in order to get a realistic image. Path tracing naturally solves this issue given the physically accurate nature of the algorithm.
The results it produces are unmatched. But they come with a major problem: rendering times. Rendering times can be crucial depending on the task at hand. Rasterization has been traditionally used in real time applications, such as video games, while path tracing is implemented in offline renderers, like the ones used for movie productions. We then need to ask one question:
Could it be possible to bring path tracing to real time?
In this project we will tackle this problem. We will build a physically based rendering engine based on path tracing with modern hardware in order to produce a software capable of producing realistic images in mere milliseconds.
As one could imagine, this task it not an easy one. In order to achieve it, we will need to understand multiple aspects of different fields: from mathematics to computer imaging, with some light notions from physics.
Chapter 1 will set the fundamentals of what ray tracing is, how a ray works, and how it intersects with an object.
In chapter 2 we will study the basics of radiometry and light transport, the field of physics that deals with the interaction between light and matter. We will introduce how photons work, how they are emitted from light sources and how they travel through the environment. We will also need to understand the mathematical abstractions in which we represent these radiometric quantities. Then, we will need to analyse how light interacts with matter, which, in a nutshell, can be described by the bidirectional scattering distribution function of the material surface and the outgoing direction of photons (since light can be either scattered or transmitted). At the end of the chapter we will obtain the most important equation in computer graphics: the rendering equation, which can be described as
\[ L_o(p, \omega_o) = L_e(p, \omega_o) + \int_{H^2(\mathbf{n})}{f(p, \omega_o \leftarrow \omega_i) L_i(p, \omega_i) \cos\theta_i\ d\omega_i} \]
Since reality is an absurdly complex –yet simple– set of rules, we will need to find a way of making the computations viable in real time. That is why in chapter 3 we will explore how random sampling can be used to generate approximations of radiometric integrals. We will start with a brief summary of random variables. Then, we will introduce Monte Carlo techniques, which rely on sampling random variables from certain distributions (usually the uniform between 0 and 1) and averaging these samples to obtain the expected value of some other distribution. This will allow us to compute integrals relatively easily at the cost of some error. In order to improve these estimations, we will study how different methods can be used to reduce the variance of the estimator, such as (multiple) importance sampling, russian roulette, or next-event estimation.
Once the theory is out of the way, it will be time to build an application. Chapter 4 will cover the implementation of the engine. We will first introduce our main set of tools, which will be Vulkan graphics API and Nvidia DesignWorks’ nvpro-samples framework (NVIDIA 2022b). Then, we will learn about the structures that make real time ray tracing possible, such as the Top and Bottom-Level Acceleration Structures (TLAS and BLAS respectively) and the Shader Binding Table (SBT). We will also understand how the ray tracing pipepline works, what types of shaders are there and how we can use them to render a scene. Materials and light sources will also need to be explained since they are a key component of the scene. Finally, we will implement some techniques which allow us to reduce the noise of the final image, such as gamma correction and temporal accumulation of frames.
Now that we have a working engine, it is time to play with it. Chapter 5 will exhibit the results of our work, comparing different scenes that showcase a variety of physical phenomena. We will also analyse how it performs in terms of image quality and frame time based on a set of parameters, like ray depth, number of samples taken on each frame, and resolution. Finally, we will compare our implementation with Peter Shirley’s engine developed in Ray Tracing In One Weekend series (Shirley 2020a) (Shirley 2020b) (Shirley 2020a).
We will end the project with the conclusions that can be drawn from the results of our work, as well as show what could be done to improve the engine in the future. To summarize, we’ve found that the engine could improve its sampling stategy. The images it produces are very noisy and need a considerable amount of samples to become sharp. This is mainly due to the weak light interface that has been implemented, since it doesn’t take into account emissive materials found in the scene. Nevertheless, the combination of how fast it can render a frame and the ability to mix multiple accumulated frames over time manages to overcome this issue. Other areas that could be further improved include the material interface and the main engine class, which presents a high degree of coupling.
The contents of this document, the Vulkan project, an In One Weekend implementation, as well as other utilities can be found in the following repository:
https://github.com/Asmilex/Raytracing
Keywords: raytracing, ray tracing, path tracing, Monte Carlo methods, Monte Carlo integration, light transport, global illumination, Vulkan.
A mi familia por su apoyo constante y permitirme empezar una carrera que ni siquiera sabía que quería.
A Augusta, Blanca, Cristina, Jorge, José “OC”, Juan Antonio, Lucas, Manu “Nomad”, Mari, Marina, Mapachana, Paula, Sarah, y Sergio por el apoyo, así como por ayudarme con el contenido, feedback del desarrollo y diseño de la documentación.
Este trabajo puede visualizarse en la web asmilex.github.io/Raytracing o en el PDF disponible en el repositorio del trabajo github.com/Asmilex/Raytracing. La página web contiene recursos adicionales como vídeos.
Ser capaces de capturar un momento.
Desde tiempos inmemoriales, este ha sido uno de los sueños de la humanidad. La capacidad de retener lo que ven nuestros ojos comenzó con simples pinturas ruprestres que nuestros ancestros dejaron enmarcadas en las paredes de sus hogares.
Con el tiempo, la tecnología evolucionó; lo cual propició formas más realistas de representar la realidad. El físico árabe Ibn al-Haytham, a finales de los años 900, describió el efecto de la cámara oscura (Encyclopedia 2022), un efecto óptico mediante el cual se puede proyectar una imagen invertida en una pared. A inicios del siglo XVIII, Nicéphore Niépce consiguió arreglar una imagen capturada por las primeras cámaras. Era una impresión primitiva, por supuesto; pero funcional. A finales de este siglo, sobre los años 1890, la fotografía se extendió rápidamente en el espacio del consumidor gracias a la compañía Kodak. Finalmente, a mediados del siglo XX la fotografía digital, la cual simplificaría muchos de los problemas de las cámaras tradicionales.
Una vez entró de lleno la era digital, los ordenadores personales se volvieron una herramienta indispensable. Con ellos, los usuarios eran capaces de mostrar imágenes en pantalla, que cambiaban bajo demanda. Naturalmente, debido a nuestro afán por recrear el mundo, nos hicimos una pregunta: ¿Podríamos simular la vida real?
Como era de esperar, este objetivo es complicado de lograr. Para conseguirlo, hemos necesitado crear abstracciones de conceptos que nos resultan naturales, como objetos, luces y seres vivos. “Cosas” que un ordenador no entiende, y sin embargo, para nosotros funcionan. Así, nació la geometría, los puntos de luces, texturas, sombreados, y otros elementos de un escenario digital. Pero estas abstracciones por sí mismas no son suficientes. Necesitamos visualizarlas.
Para solventar este problema existen diferentes algoritmos. El más primitivo es rasterización, una técnica utilizada para convertir objetos tridimensionales de una escena en un conjunto de píxeles. Proyectando acordemente el entorno a una cámara, conseguimos colorear una región del espacio, de forma que en conjunto representan un punto de vista de un mundo digital. Su simplicidad lo convierte en una manera extraordinariamente rápida de conseguir una imagen. Sin embargo, su gran inconveniente es la fidelidad. Debido a su naturaleza (que se basa en una simple proyección), este algoritmo está extremadamente limitado. Para aumentar el realismo del producto final, con el tiempo se idearon métodos como shadow mapping, precómputo de luces, o reflection cubemaps, los cuales intentan solventar el problema subyacente de rasterización: conocer el entorno de la escena.
Como era de esperar, se buscaron vías alternativas a rasterización para producir una imagen. La que más destacó fue ray tracing. Su primer uso documentado data de los años 60, en un artículo de Appel (Freniere and Tourtellott 1997). Parte de una idea increíblemente simple: consiste en disparar un rayo desde una cámara para comprobar si un objeto está ocluído. De esta forma, se resuelve el problema de conocer qué es lo que se ve desde la cámara.
Un par de décadas más tarde, sobre 1980, comienzan a ser publicadas imágenes hechas por ray tracing muy realistas. En estos años también se experimenta un crecimiento en el número de publicaciones sobre cómo hacer más rápido ray tracing. Uno de los puntos clave fue reducir el tiempo requerido para calcular intersecciones con objetos, pues suponen hasta el 95% del cómputo total. Kay y Kajiya publican un tipo de estructura denominada bounding box que simplifica este problema de manera considerable.

En 1986 Kajiya introdujo la denominada rendering equation (Kajiya 1986). Esta es una ecuación que modela analíticamente la cantidad de luz de un cierto basándose en las propiedades del material y la luz que llega a dicho punto.
\[ L_o(p, \omega_o) = L_e(p, \omega_o) + \int_{H^2(\mathbf{n})}{f(p, \omega_o \leftarrow \omega_i) L_i(p, \omega_i) \cos\theta_i\ d\omega_i} \]
Debido a la complejidad de esta ecuación, se diseñó un algoritmo denominado path tracing, el cual es capaz de estimar numéricamente su valor. Su idea principal se basa en hacer rebotar rayos por la escena una y otra vez, de forma que en cada impacto se adquiera nueva información.
Los métodos de Monte Carlo proliferaron debido a su fundamento teórico, el cual es idóneo para las diferentes formas de ray tracing. Estas técnicas se basan en el uso de muestras de alguna distribución para calcular un valor determinado. En este caso, aproximan el valor que toma la integral de la rendering equation. Comenzaron siendo utilizados en 1960 para el cálculo de la radiancia generada por los fotones en simulaciones físicas, por lo que transicionaron fácilmente a ray tracing.
A finales del siglo XX path tracing penetra de lleno en la industria. Numerosas empresas comienzan a desarrollar motores de renderizado basado en dicho algoritmo, abandonando así rasterización. Las productoras de cine empiezan a utilizar exclusivamente medios digitales para crear películas, una forma de crear arte nunca vista hasta la fecha.
La elegancia de path tracing reside en su naturaleza tan intuitiva. Pues claro que la respuesta a “¿Cómo simulamos fielmente una imagen en un ordenador?” es “Representando la luz de forma realista”. Gracias a la física sabemos que los fotones emitidos por las fuentes de iluminación se mueven por el espacio impactando en los diferentes objetos. Y, como ocurre a menudo, la respuesta a muchos de nuestros problemas ya existe en el mundo exterior. Aprendiendo sobre cómo funciona nuestro alrededor nos permitirá modelar nuevos mundos a nuestro gusto. De esta manera, podemos dejar atrás los hacks que utilizábamos en rasterización; no habrá necesidad de falsificar los efectos de iluminación, puesto que path tracing los solventa de manera natural.
Aún con todos los avances del medio, el elefante en la sala seguía siendo el rendimiento. Producir una única imagen podría suponer horas de cómputo; incluso días. A diferencia del universo, nosotros no podemos permitirnos el lujo de usar un elevado número de fotones, ni hacer rebotar la luz tantas veces como queramos. Nos pasaríamos una eternidad esperando. Y para ver una imagen en nuestra pantalla necesitaremos estar vivos, claro. En la práctica, esto supuso que no todos los medios pudieron pasarse a path tracing. Aquellas industrias como la de los videojuegos, en las que se prioriza la rapidez sobre fidelidad tuvieron que continuar usando rasterización. A fin de cuentas, solo disponen de unos escasos milisegundos para renderizar una imagen.
Sin embargo, el paso del tiempo es imparable. Las pinturas rupestres dieron paso al óleo sobre lienzo, mientras que las cámaras digitales reemplazaron a las oscuras. Es natural esperar que, en algún momento, rasterización se convierta en un algoritmo del pasado. Y ese momento es la actualidad.
En 2018 Nvidia introdujo la arquitectura de tarjetas gráficas Turing (Emmett Kilgariff 2018). Aunque por estos años ya existían implementaciones de ray tracing en gráficas (tan temprano como (Purcell et al. 2002), (Ertl et al. 2022)), esta arquitectura presenta la capacidad de realizar cómputos específicos de ray tracing acelerados por hardware en gráficas de consumidor. Esto significa que path tracing se vuelve viable en tiempo real. En lugar de horas, renderizar una imagen costará milisegundos.
Se da el pistoletazo de salida a una nueva transición.
En este trabajo se estudiarán los fundamentos de ray tracing y path tracing en tiempo real. Para conseguirlo, se han propuesto los siguientes objetivos:
Afortunadamente, se ha conseguido realizar exitosamente cada uno de los objetivos. Esta memoria cubrirá todo el trabajo que ha sido necesario realizar para lograrlo.
Esta memoria recapitulará todas las técnicas utilizadas para resolver el problema propuesto. En los primeros capítulos, estudiaremos los fundamentos teóricos, mientras que en los posteriores construiremos una implementación de ray tracing, la cual analizaremos con detalle para finalizar.
El capítulo 1 sentará las bases de ray tracing: qué es un rayo exactamente, cómo podemos representarlo matemáticamente y cuáles son las ecuaciones que nos permiten modelar la propagación e impacto con diferentes objetos.
En el capítulo 2 introduciremos los fundamentos de la radiometría y el transporte de luz, el área de la física que se encarga de la interacción entre la luz y la materia. Estudiaremos cómo funcionan los fotones, cómo son emitidos desde las denominadas fuentes de iluminación, y cómo se propagan por el medio. Para conseguirlo, necesitaremos construir ciertas abstracciones que representen propiedades radiométricas. Entre las más importantes se encuentran la potencia, la intensidad radiante y la radiancia. También será necesario el concepto de ángulos sólidos, los cuales generalizan la concepción clásica de ángulo planar.
Será entonces cuando aprendamos cómo interacciona la luz con la materia. Esto nos llevará a crear una familia específica de funciones denominadas bidirectional distribution functions, las cuales describen como se reflejan los fotones cuando impactan con una superficie. Asimismo, será importante conocer la dirección de salida de estos, por lo que habrá que estudiar los fenómenos de reflexión y refracción. Al final del capítulo obtendremos la ecuación del transporte de luz o rendering equation.
Esta ecuación modela fielmente cuánta luz existe en un punto dependiendo de su entorno. Sin embargo, es prácticamente imposible resolverla analíticamente. Por ello, con el fin de poder realizar los cálculos en tiempo real, en el capítulo 3 exploraremos las técnicas de Monte Carlo. Estas técnicas se basan en el uso de muestreo aleatorio. A partir de promediar muestras de una variable aleatoria seremos capaces de determinar, primero, la media de una transformación de una v.a.; y después, el valor de una integral. Esto nos permitirá estimar el valor de la ecuación del transporte de luz.
Sin embargo, muestrear sin cabeza no producirá resultados especialmente buenos. Por ello, comprobaremos cómo algunas técnicas reducen la varianza del estimador de Monte Carlo; y con ello, el ruido de la imagen final. Entre los métodos estudiados se encuentran el muestreo (múltiple) por importancia, la ruleta rusa, el muestreo directo de fuentes de iluminación o los métodos de Quasi-Monte Carlo. Todos estos los acabaremos enfocando al área que estamos explorando.
Cuando hayamos acabado con la teoría física y matemática, será el momento de producir la aplicación. El capítulo 4 cubirá la construcción de un motor de renderizado físicamente realista. Presentaremos algunas herramientas clave en la resolución del problema; entre las que se encuentran Vulkan, una interfaz de programación de aplicaciones gráfica, y el framework para Vulkan Ray tracing de Nvidia DesignWorks denominado nvpro-samples (NVIDIA 2022a).
Debido a la gran complejidad del problema, será necesario introducir algunas estructuras clave que habilitan la ejecución de ray tracing en tiempo real. Las dos más destacables son la Top y Bottom-Level Acceleration Structures (TLAS y BLAS, respectivamente), que albergan información sobre la geometría de una escena; y la Shader Binding Table (SBT), una estructura que permite seleccionar shaders dinámicamente a partir de la intersección de los rayos.
Será entonces cuando hablemos de cómo funciona la ray tracing pipeline, qué tipos de shaders existen y cómo podemos usarlos para renderizar una escena. Además, hablaremos sobre cómo hemos representado los materiales y las fuentes de iluminación. Finalmente, veremos algunas técnicas adicionales que hemos usado para reducir el ruido de la imagen, como la corrección de gamma y acumulación temporal de frames.
Una vez tengamos un motor funcional, será hora de jugar con él. El capítulo 5 mostrará los resultados de nuestro trabajo. Visualizaremos algunos fenómenos físicos que hemos estudiado a lo largo de la memoria. Estos serán encapsulados en aproximadamente una docena de escenas, centrándose cada una en cierta particularidad; como puede ser la iluminación global, la refracción y reflexión, o el comportamiento de materiales específicos.
También analizaremos cómo rinde el motor en términos de calidad visual de imagen y tiempo de renderizado. Para ello, comprobaremos cómo varían estas dos métricas al cambiar los parámetros del algoritmo path tracing y las técnicas de reducción de ruido. Entre estos parámetros, se encuentran el número de muestras del estimador de Monte Carlo, la profunidad de rebotes de un rayo, la acumulación temporal y la resolución.
Para poner en contexto el rendimiento, compararemos nuestra implementación con el path tracer desarollado en los libros de Peter Shirley Ray Tracing In One Weekend series (Shirley 2020a) (Shirley 2020b) (Shirley 2020a).
Terminaremos el grueso del trabajo con el capítulo de conclusiones. Reflexionaremos sobre todo lo que hemos aprendido; desde los éxitos logrados hasta las dificultades que presenta este complejo algoritmo. Además, explicaremos cómo se podría mejorar este trabajo, analizando de qué pie cojea la implementación.
En los anexos se puede encontrar contenido adicional. El primer anexo cubre el estado del arte del área –aunque este trabajo es prácticamente estado del arte–. En el segundo hablaremos sobre cómo se ha realizado este trabajo: desde las principales influencias hasta el diseño gráfico; pasando por el presupeusto y los ciclos de desarrollo. Por último, se ha incluído un glosario de términos y conceptos para facilitar la lectura de este documento.
Aunque en la realización de este trabajo se han utilizado múltiples fuentes de información, destacan una serie de libros por encima del resto:
Empecemos por definir lo que es un rayo.
Un rayo (Shirley 2020a) es una función \(P(t) = \mathbf{\mathbf{o}} + t\mathbf{d}\), donde \(\mathbf{\mathbf{o}}\) el origen, un punto del espacio afín; \(\mathbf{d}\) un vector libre, y \(t \in \mathbb{R}\). Podemos considerarlo una interpolación entre dos puntos en el espacio, donde \(t\) controla la posición en la que nos encontramos.
Por ejemplo, si \(t = 0\), obtendremos el origen. Si \(t = 1\), obtendremos el punto correspondiente a la dirección. Usando valores negativos vamos hacia atrás.
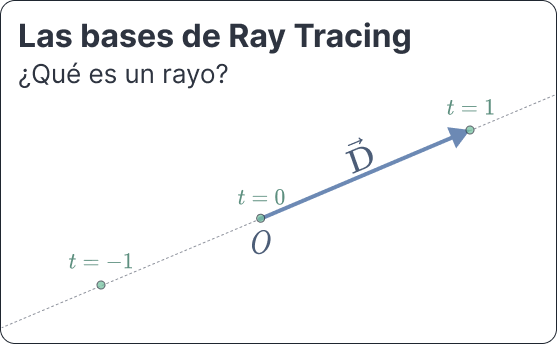
Dado que estos puntos estarán generalmente en \(\mathbb{R}^3\), podemos escribirlo como
\[ P(t) = (o_x, o_y, o_z) + t (d_x, d_y, d_z) \](1)
Estos rayos los dispararemos a través de una cámara virtual, que estará enfocando a la escena. De esta forma, los haremos rebotar con los objetos que se encuentren en el camino del rayo. a este proceso lo llamaremos ray casting.
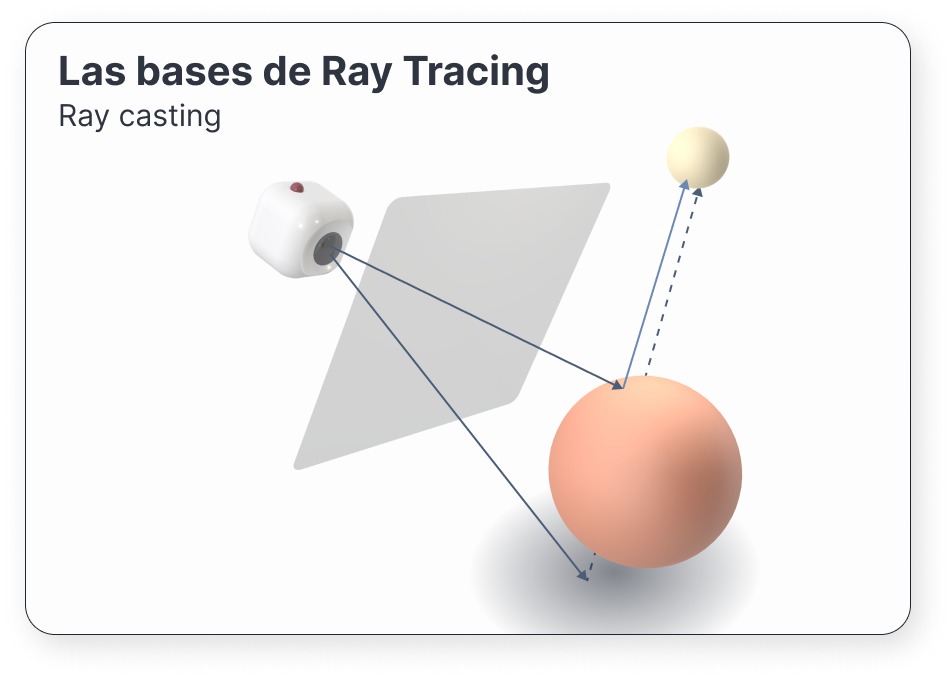
Generalmente, nos quedaremos con el primer objeto que nos encontremos en su camino. Aunque, a veces, nos interesará saber todos con los que se encuentre.
Cuando un rayo impacta con un objeto, adquirirá parte de las propiedades lumínicas del punto de impacto. Por ejemplo, cuánta luz proporciona la lámpara que tiene encima la esfera de la figura anterior.
Una vez recojamos la información que nos interese, aplicaremos otro raycast desde el nuevo punto de impacto, escogiendo una nueva dirección determinada. Esta dirección dependerá del tipo de material del objeto. Y, de hecho, algunos serán capaces de invocar varios rayos.
Por ejemplo, los espejos reflejan la luz casi de forma perfecta; mientras que otros elementos como el agua o el cristal reflejan y refractan luz, así que necesitaremos generar dos nuevos raycast.
Usando suficientes rayos obtendremos la imagen de la escena. a este proceso de ray casting recursivo es lo que se conoce como ray tracing.
Como este proceso puede continuar indefinidamente, tendremos que controlar la profundidad de la recursión. a mayor profundidad, mayor calidad de imagen; pero también, mayor tiempo de ejecución.
Una de las partes más importantes de ray tracing, y a la que quizás dedicaremos más tiempo, es a la elección de la dirección.
Hay varios factores que entran en juego a la hora de decidir qué hacemos cuando impactamos con un nuevo objeto:
Estas cuestiones las exploraremos a fondo en las siguientes secciones.
Como dijimos al principio del capítulo, representaremos un rayo como
\[ \begin{aligned} P(t) & = (o_x, o_y, o_z) + t (d_x, d_y, d_z) = \\ & = (o_x + t d_x, o_y + t d_y, o_y + t d_z) \end{aligned} \]
Por ejemplo, tomando \(\mathbf{\mathbf{o}} = (1, 3, 2), \mathbf{d} = (1, 2, 1)\):
Nos resultará especialmente útil limitar los valores que puede tomar \(t\). Restringiremos los posibles puntos del dominio de forma que \(t \in [t_{min}, t_{max})\), con \(t_{min} < t_{max}\). En general, nos interesará separarnos de las superficies un pequeño pero no despreciable \(\varepsilon\) para evitar intersecar con el origen.
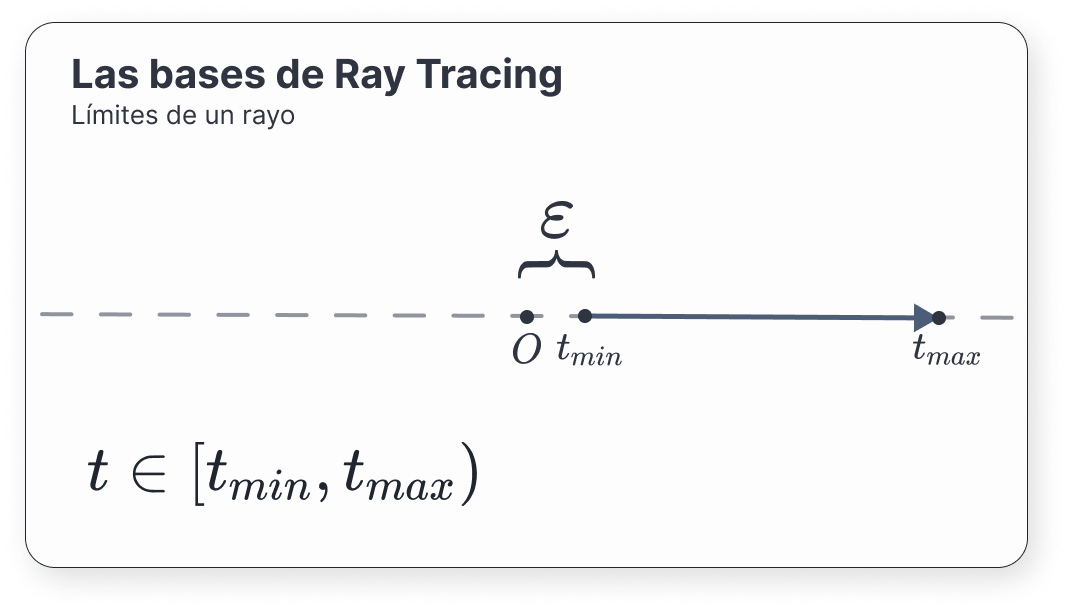
Una de las principales cuestiones que debemos hacernos es saber cuándo un rayo impacta con una superficie. Lo definiremos analíticamente.
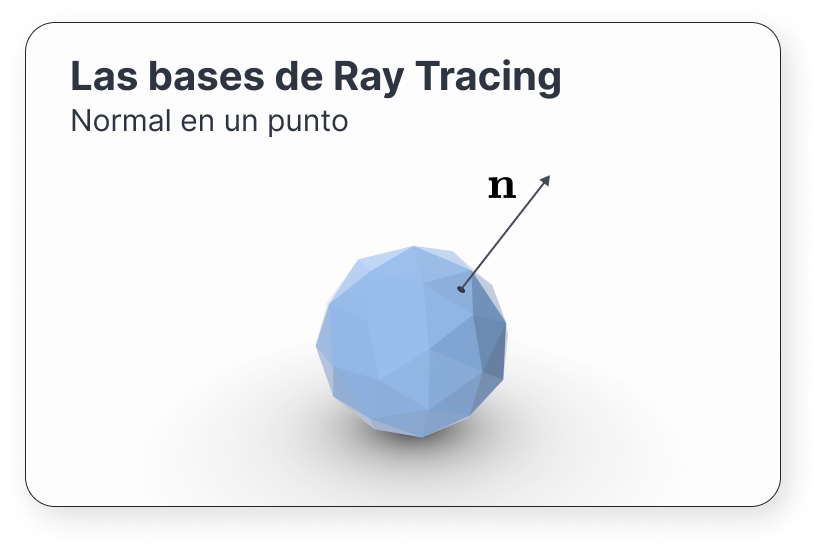
Generalmente, cuando hablemos de superficies, nos referiremos superficies diferenciables, pues nos interesará conocer el vector normal en cada punto.
Una superficie implícita es una superficie en un espacio euclidiano definida como
\[ F(x, y, z) = 0 \]
Esta ecuación implícita define una serie de puntos del espacio \(\mathbb{R}^3\) que se encuentran en la superficie. Por ejemplo, la esfera se define como \(x^2 + y^2 + z^2 - 1 = 0\).
Consideremos una superficie \(S\) y un punto regular \(\mathbf{\mathbf{p}}\) de ella; es decir, un punto tal que el gradiente de \(F\) en \(\mathbf{\mathbf{p}}\) no es 0. Se define el vector normal \(\mathbf{n}\) a la superficie en ese punto como
\[ \mathbf{n} = \nabla F(\mathbf{p}) = \left( \frac{\partial F(\mathbf{p})}{\partial x}, \frac{\partial F(\mathbf{p})}{\partial y}, \frac{\partial F(\mathbf{p})}{\partial z}\right ) \](2)
Dado un punto \(\mathbf{q} \in \mathbb{R}^3\), queremos saber dónde interseca un rayo \(P(t)\). Es decir, para qué \(t\) se cumple que \(F(P(t)) = 0 \iff F(\mathbf{\mathbf{o}} + t\mathbf{d}) = 0\).
Este tipo de superficies suele requerir un cálculo numérico iterativo por lo general, pero algunos objetos presentan expresiones sencillas que permiten una resolución analítica.
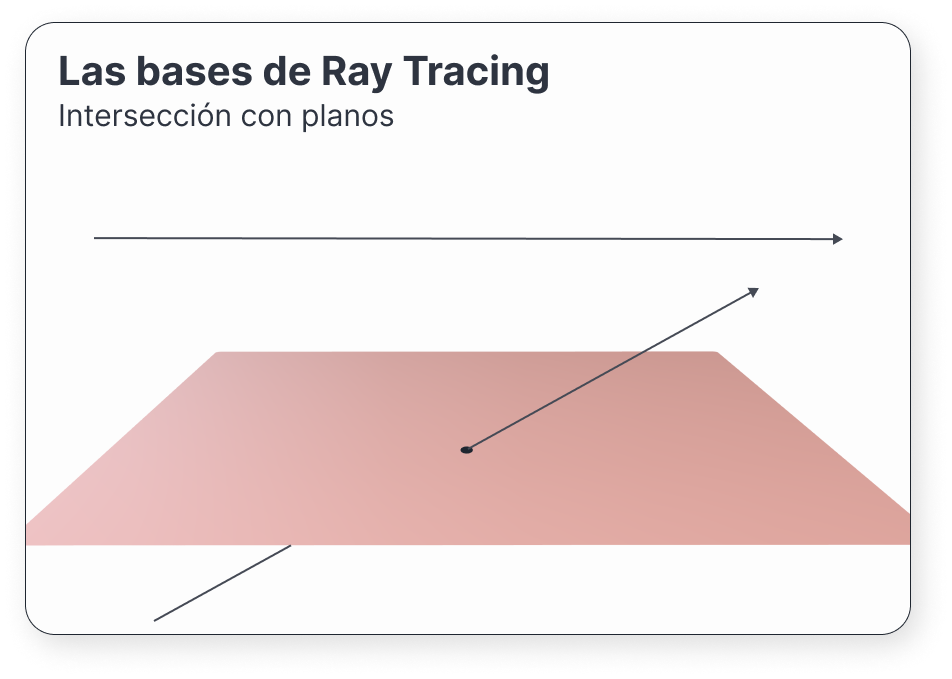
Este es el caso de los planos. Para comprobarlo, tomemos un punto \(\mathbf{q}_0\) de un cierto plano y un vector normal a la superficie \(\mathbf{n}\). La ecuación implícita del plano será (Shirley and Morley 2003)
\[ F(Q) = (\mathbf{q} - \mathbf{q}_0) \cdot \mathbf{n} = 0 \]
Si pinchamos nuestro rayo en la ecuación,
\[ \begin{aligned} F(P(t)) & = (P(t) - \mathbf{q}_0) \cdot \mathbf{n} \\ & = (\mathbf{\mathbf{o}} + t\mathbf{d} - \mathbf{q}_0) \cdot \mathbf{n} = 0 \\ \end{aligned} \]
Resolviendo para \(t\), esto se da si
\[ \begin{aligned} \mathbf{\mathbf{o}} \cdot \mathbf{n} + t\mathbf{d} \cdot \mathbf{n} - \mathbf{q}_0 \cdot \mathbf{n} & = 0 & \iff \\ t\mathbf{d} \cdot \mathbf{n} & = \mathbf{q}_0 \cdot \mathbf{n} - \mathbf{\mathbf{o}} \cdot \mathbf{n} & \iff \\ t & = \frac{\mathbf{q}_0 \cdot \mathbf{n} - \mathbf{\mathbf{o}} \cdot \mathbf{n}}{\mathbf{d} \cdot \mathbf{n}} \end{aligned} \]
Es decir, hemos obtenido el único valor de \(t\) para el cual el rayo toca la superficie.
Debemos tener en cuenta el caso para el cual \(d \cdot \mathbf{n} = 0\). Esto solo se da si la dirección y el vector normal a la superficie son paralelos.
Otra forma de definir una superficie en el espacio es mediante un subconjunto \(S \subset \mathbb{R}^2\) y una serie de funciones, \(f, g, h: S \rightarrow \mathbb{R}^3\), de forma que
\[ (x, y, z) = \left( f(u, v), g(u, v), h(u, v) \right) \\ \]
En informática gráfica, hacemos algo similar cuando mapeamos una textura a una superficie. Se conoce como UV mapping.
Demos un par de ejemplos de superficies paramétricas:
El vector normal \(\mathbf{n}\) a la superficie en un punto \((u, v)\) del dominio viene dado por
\[ \mathbf{n}(u, v) = \left( \frac{\partial f}{\partial u}, \frac{\partial g}{\partial u}, \frac{\partial h}{\partial u} \right) \times \left( \frac{\partial f}{\partial v}, \frac{\partial g}{\partial v}, \frac{\partial h}{\partial v} \right) \]
El punto de intersección de una superficie paramétrica con un rayo viene dado por aquellos puntos de la superifice \((u, v)\) para los que
\[ \begin{aligned} \begin{cases} o_x + td_x = f(u, v) \\ o_y + td_y = g(u, v) \\ o_z + td_z = h(u, v) \end{cases} \end{aligned} \]
Con \(t \in \mathbb{R}\). Es posible que el rayo no impacte en ningún punto. En ese caso, el sistema de ecuaciones no tendría solución. Otra posibilidad es que intersequen en varios puntos.
Por regla general este tipo de superficies no permiten un cálculo fácil del punto de intersección, lo cual hace que se evitan en ray tracing. En su lugar se opta por otro tipo de estructuras como las mallas de triángulos.
Estudiemos ahora cómo intersecan una esfera con nuestro rayo (Shirley and Morley 2003). Una esfera de centro \(\mathbf{c}\) y radio \(r\) viene dada por aquellos puntos \(\mathbf{p} = (x, y, z)\) que cumplen
\[ (\mathbf{p} - \mathbf{c}) \cdot (\mathbf{p} - \mathbf{c}) = r^2 \]
Podemos reescribir esta ecuación en términos de sus coordenadas para obtener
\[ (x - c_x)^2 + (y - c_y)^2 + (z - c_z)^2 = r^2 \]
Veamos para qué valores de \(t\) de nuestro rayo se cumple esa ecuación:
\[ \begin{aligned} (P(t) - \mathbf{c}) \cdot (P(t) - \mathbf{c}) & = r^2 & \iff \\ (\mathbf{o} + t\mathbf{d} - \mathbf{c}) \cdot (\mathbf{o} + t\mathbf{d} - \mathbf{c}) & = r^2 & \iff \\ \end{aligned} \]
Aplicando las propiedades del producto escalar de la conmutatividad (\(\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}\)) y la distributiva (\(\mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c}\)), podemos escribir
\[ \begin{aligned} ((\mathbf{o} - \mathbf{c}) + t\mathbf{d}) \cdot ((\mathbf{o} - \mathbf{c}) + t\mathbf{d}) & = r^2 & \iff \\ (\mathbf{o} - \mathbf{c})^2 + 2 \cdot (\mathbf{o} - \mathbf{c}) \cdot t\mathbf{d} + (t\mathbf{d})^2 & = r^2 & \iff \\ d^2t^2 + 2 d \cdot (\mathbf{o} - \mathbf{c})t + (\mathbf{o} - \mathbf{c})^2 - r^2 & = 0 & \iff \\ \end{aligned} \]
Así que tenemos una ecuación de segundo grado. Resolviéndola, nos salen nuestros puntos de intersección:
\[ t = \frac{ - d \cdot (\mathbf{o} - \mathbf{c}) \pm \sqrt{(d \cdot (\mathbf{o} - \mathbf{c}))^2 - 4 (\mathbf{d}^2)((\mathbf{o} - \mathbf{c})^2 - r^2)} }{ 2 \mathbf{d}^2 } \]
Debemos distinguir tres casos, atiendiendo al valor que toma el discriminante \(\Delta = \small{(\mathbf{d} \cdot (\mathbf{o} - \mathbf{c}))^2 - 4 (\mathbf{d}^2)((\mathbf{o} - \mathbf{c})^2 - r^2)}\):
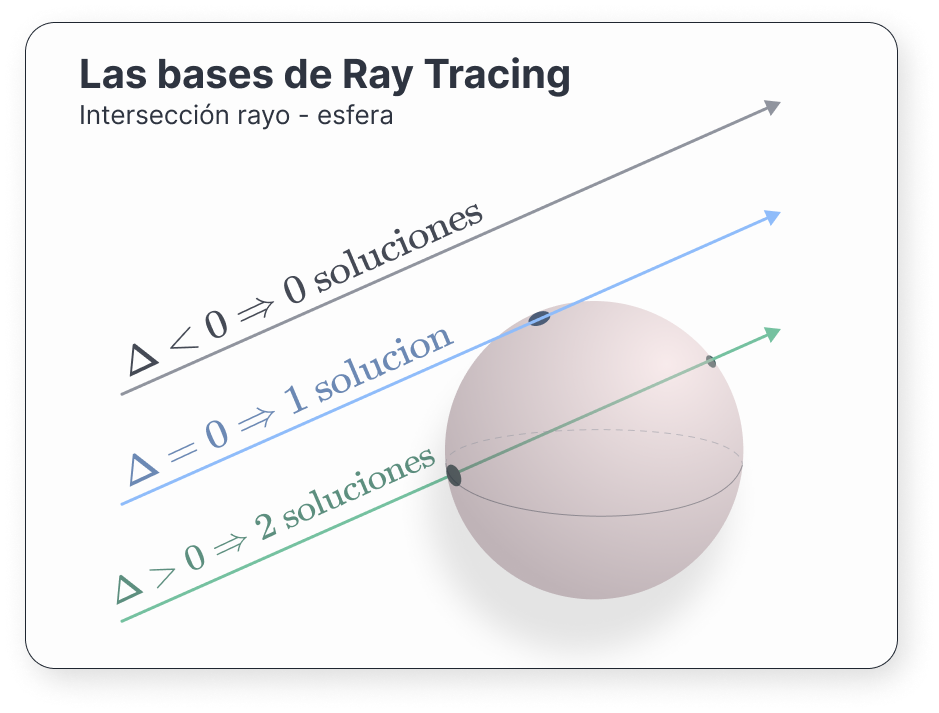
Para estos dos últimos, si consideramos \(t_0\) cualquier solución válida, el vector normal resultante viene dado por
\[ \mathbf{n} = 2 (P(t_0) - \mathbf{c}) \]
o, normalizando,
\[ \hat{\mathbf{n}} = \frac{(P(t_0) - \mathbf{c})}{r} \]
Este tipo de intersecciones serán las más útiles en nuestro path tracer. Generalmente, nuestras geometrías estarán compuestas por mallas de triángulos, así que conocer dónde impacta nuestro rayo será clave. Empecemos por la base:
Un triángulo viene dado por tres puntos, \(a, \mathbf{b}\), y \(\mathbf{c}\); correspondientes a sus vértices. Para evitar casos absurdos, supongamos que estos puntos son afinmente independientes; es decir, que no están alineados.
Podemos describir los puntos contenidos en el plano que forman estos vertices mediante coordenadas baricéntricas. Este sistema de coordenadas expresa cada punto del plano como una combinación convexa de los vértices \(\mathbf{a}, \mathbf{b}, \mathbf{c}\) (Shirley and Morley 2003). Es decir, que para cada punto \(\mathbf{p}\) del triángulo existen \(\alpha, \beta\) y \(\gamma\) tales que \(\alpha + \beta + \gamma = 1\) y
\[ \mathbf{p} = \alpha a + \beta \mathbf{b} + \gamma \mathbf{c} \]
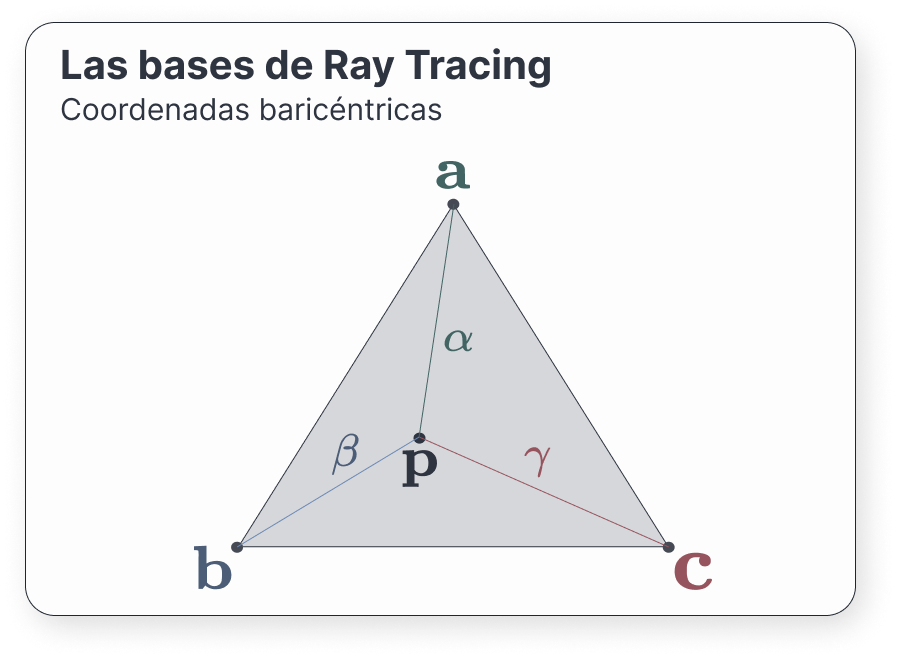
Debemos destacar que existen dos grados de libertad debido a la restricción de que las coordenadas sumen 1.
Una propiedad de estas coordenadas que nos puede resultar útil es que un punto \(\mathbf{p}\) está contenido en el triángulo si y solo si \(0 < \alpha, \beta, \gamma < 1\).
Esta propiedad y la restricción de que sumen 1 nos da una cierta intuición de cómo funcionan. Podemos ver las coordenadas baricéntricas como la contribución de los vértices a un punto \(\mathbf{p}\). Por ejemplo, si \(\alpha = 0\), eso significa que el punto viene dado por \(\beta \mathbf{b} + \gamma \mathbf{c}\); es decir, una combinación lineal de \(\mathbf{b}\) y \(\mathbf{c}\). Se encuentra en la recta que generan.
Por proponer otro ejemplo, si alguna de las coordenadas fuera mayor que 1, eso significaría que el punto estaría más allá del triángulo.
Podemos eliminar una de las varibales escribiendo \(\alpha = 1 - \beta - \gamma\), lo que nos dice
\[ \begin{aligned} \mathbf{p} & = (1 - \beta - \gamma) \mathbf{a} + \beta \mathbf{b} + \gamma \mathbf{c} \\ & = \mathbf{a} + (\mathbf{b} - \mathbf{a}) \beta + (\mathbf{c} - \mathbf{a}) \gamma \end{aligned} \]
bajo la restricción
\[ \begin{aligned} \beta + \gamma & < 1 \\ 0 & < \beta \\ 0 & < \gamma \end{aligned} \](3)
Un rayo \(P(t) = \mathbf{o} + t\mathbf{d}\) impactará en un punto del triángulo si se cumple
\[ P(t) = \mathbf{o} + t\mathbf{d} = \mathbf{a} + (\mathbf{b} - \mathbf{a}) \beta + (\mathbf{c} - \mathbf{a}) \gamma \]
cumpliendo [3]. Podemos expandir la ecuación anterior en sus coordenadas para obtener
\[ \begin{aligned} o_x + td_x & = a_x + (b_x - a_x) \beta + (c_x - a_x) \gamma \\ o_y + td_y & = a_y + (b_y - a_y) \beta + (c_y - a_y) \gamma \\ o_z + td_z & = a_z + (b_z - a_z) \beta + (c_z - a_z) \gamma \\ \end{aligned} \]
Reordenamos:
\[ \begin{aligned} (a_x - b_x) \beta + (a_x - c_x) \gamma+ td_x & = a_x - o_x \\ (a_y - b_y) \beta + (a_y - c_y) \gamma+ td_y & = a_y - o_y \\ (a_z - b_z) \beta + (a_z - c_z) \gamma+ td_z & = a_z - o_z \end{aligned} \]
Lo que nos permite escribir el sistema en forma de ecuación:
\[ \begin{pmatrix} a_x - b_x & a_x - c_x & d_x \\ a_y - b_y & a_y - c_y & d_y \\ a_z - b_z & a_z - c_z & d_z \end{pmatrix} \begin{pmatrix} \beta \\ \gamma \\ t \end{pmatrix} = \begin{pmatrix} a_x - o_x \\ a_y - o_y \\ a_z - o_z \end{pmatrix} \]
Calcular rápidamente la solución a un sistema de ecuaciones lineales es un problema habitual. En (Shirley and Morley 2003) se utiliza la regla de Cramer para hacerlo, esperando que el compilador optimice las variables intermedias creadas. Nosotros no nos tendremos que preocupar de esto en particular, ya que el punto de impacto lo calculará la GPU gracias a las herramientras aportadas por KHR (The Khronos Vulkan Working Group 2022, Ray Traversal).
Para obtener el vector normal, podemos hacer el producto vectorial de dos vectores que se encuentren en el plano del triángulo. como, por convención, los vértices se guardan en sentido antihorario visto desde fuera del objeto, entonces
\[ \mathbf{n} = (\mathbf{b} - \mathbf{a}) \times (\mathbf{c} - \mathbf{a}) \]
En este capítulo estudiaremos las bases de la radiometría. Esta área de la óptica nos proporcionará una serie de herramientas con las cuales podremos responder a la pregunta cuánta luz existe en un punto.
Antes de comenzar a trabajar, necesitamos conocer qué entendemos por luz. Aunque hay muchas formas de trabajar con ella (a fin de cuentas, todavía seguimos discutiendo sobre qué es exactamente la luz 1), nosotros nos quedaremos con la definición clásica y algunas pinceladas de la cuántica. Nos será suficiente utilizar el concepto de fotón.
Un fotón es aquella particula emitida por una fuente de iluminación. Estos fotones tienen una posición, una dirección de propagación y una longitud de onda \(\lambda\) (Shirley and Morley 2003); así como una velocidad \(c\) que depende del índice de refracción del medio, \(n\). La unidad de medida de \(\lambda\) es el nanómetro (\(\text{nm}\)).
Nota(ción): cuando usemos un paréntesis tras una ecuación, dentro denotaremos sus unidades de medida.
Necesitaremos también definir qué es la frecuencia, \(f\). Su utilidad viene del hecho de que, cuando la luz cambia de medio al propagarse, la frecuencia se mantiene constante.
\[ f = \frac{c}{\lambda} (\text{Hz}) \](4)
Un fotón tiene asociada una carga de energía, denotada por \(Q\):
\[ Q = hf = \frac{hc}{\lambda} (\text{J}) \](5)
donde \(h = 6.62607004 \times 10^{-34} \text{J} \cdot \text{s}\) es la constante de Plank y \(c = 299 792 458 \text{ m/s}\) la velocidad de la luz.
En realidad, todas estas cantidades deberían tener un subíndice \(\lambda\), puesto que dependen de la longitud de onda. La energía de un fotón \(Q\), por ejemplo, debería denotarse \(Q_\lambda\). Sin embargo, en la literatura de informática gráfica se suele optar por omitirla, puesto que la mayoría de motores no generalizan las particularidades de cada longitud de onda. ¡Tenlo en cuenta a partir de aquí!
A partir de la energía \(Q\), podemos estimar la cantidad total de energía que pasa por una región del espacio por unidad de tiempo. A esta tasa la llamaremos potencia, o flujo radiante \(\Phi\) (Pharr, Jakob, and Humphreys 2016, Radiometry). Esta medida nos resultará más útil que la energía total, puesto que nos permite estimar la energía en un instante:
\[ \Phi = \lim_{\Delta t \to 0}{\frac{\Delta Q}{\Delta t}} = \frac{dQ}{dt} (\text{J/s}) \](6)
Su unidad es julios por segundo, comúnmente denotado vatio (watts, \(\text{W}\)). También se utiliza el lumen. Podemos encontrar la energía total en un periodo de tiempo \([t_0, t_1]\) integrando el flujo radiante:
\[ Q = \int_{t_0}^{t_1}{\Phi(t)dt} \]
La irradiancia o radiancia emitida es la potencia por unidad de área que recibe una región de una superficie o un punto de la misma. Si \(A\) es el área de dicha superficie, la irradiancia se define como
\[ E = \frac{\Phi}{A} (\text{W/m}^2) \](7)
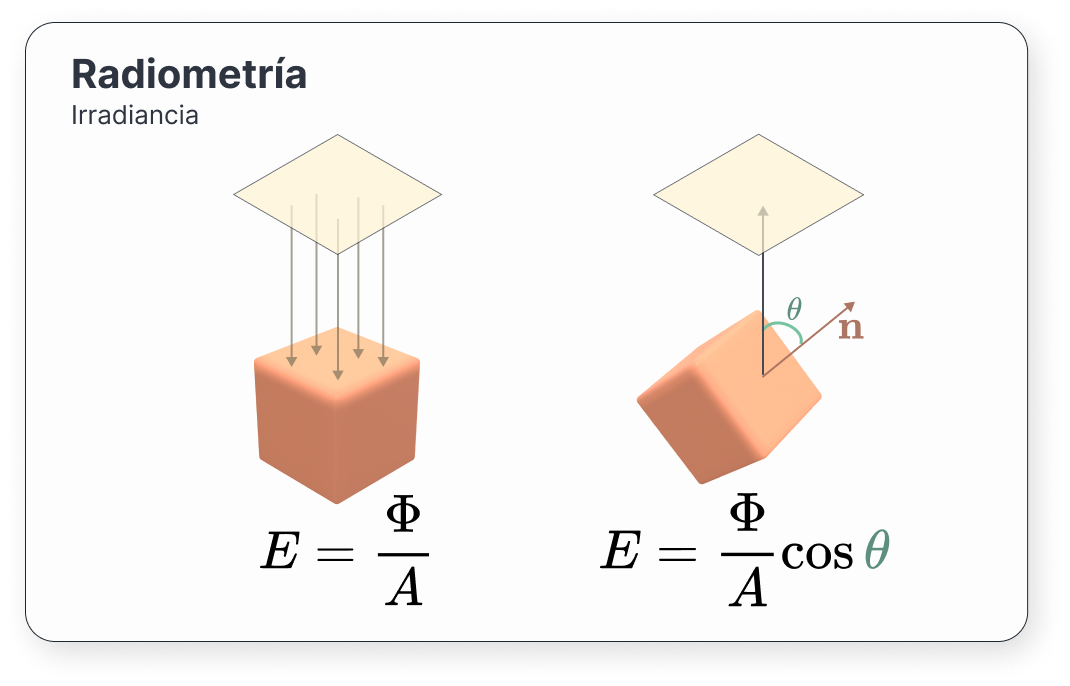
Ahora que tenemos la potencia emitida en una cierta área, nos surge una pregunta: ¿y en un cierto punto \(p\)?.
Tomando límites en la expresión anterior, encontramos la respuesta:
\[ E(p) = \lim_{\Delta A \to 0}{\frac{\Delta \Phi}{\Delta A}} = \frac{d\Phi}{dA} (\text{W/m}^2) \](8)
De la misma manera que con la potencia, integrando \(E(p)\) podemos obtener el flujo radiante:
\[ \Phi = \int_{A}{E(p)dp} \]
El principal problema de la irradiancia es que no nos dice nada sobre las direcciones desde las que ha llegado la luz.
Con estas tres unidades básicas, nos surge una pregunta muy natural: ¿cómo mido cuánta luz llega a una superficie?
Para responder a esta pregunta, necesitaremos los ángulos sólidos. Son la extensión de los ángulos bidimensionales a los que estamos acostumbrados (llamados técnicamente ángulos planares).
Ilustremos el sentido de estos ángulos: imaginemos que tenemos un cierto objeto en dos dimensiones delante de nosotros, a una distancia desconocida. ¿Sabríamos cuál es su tamaño, solo con esta información? Es más, si entrara otro objeto en la escena, ¿podríamos distinguir cuál de ellos es más grande?
Parece difícil responder a estas preguntas. Sin embargo, sí que podemos determinar cómo de grandes nos parecen desde nuestro punto de vista. Para ello, describimos una circunferencia de radio \(r\) alrededor nuestra. Si trazamos un par de líneas desde nuestra posición a las partes más alejadas de este objeto, y las cortamos con nuestra circunferencia, obtendremos un par de puntos inscritos en ella. Pues bien, al arco que encapsulan dichos puntos le vamos a hacer corresponder un cierto ángulo: el ángulo planar.
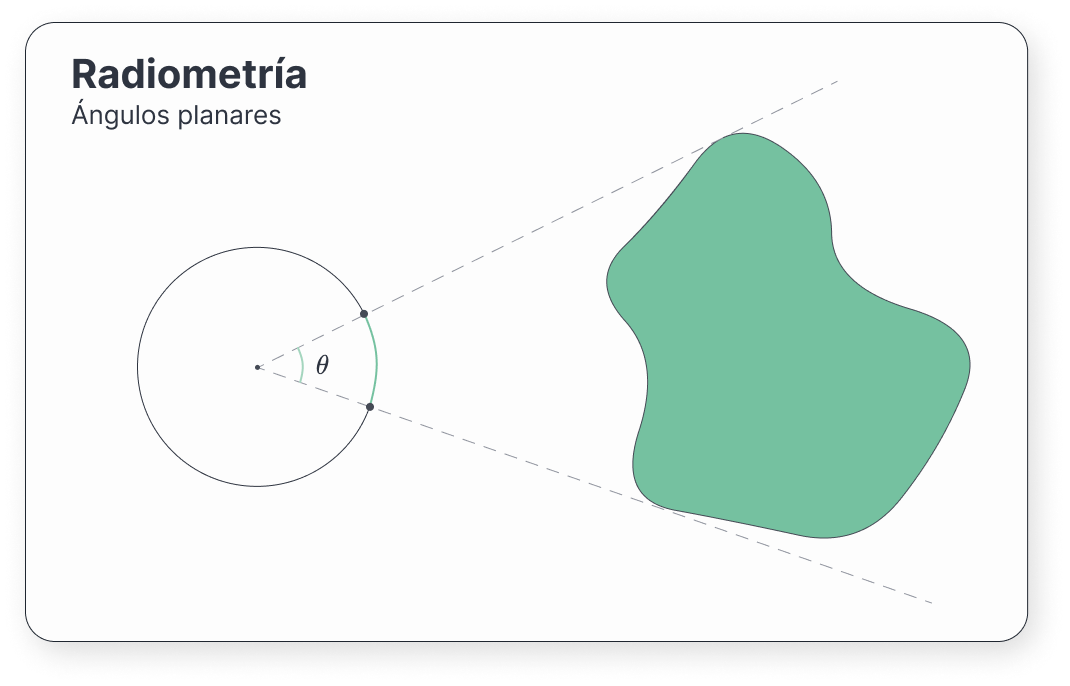
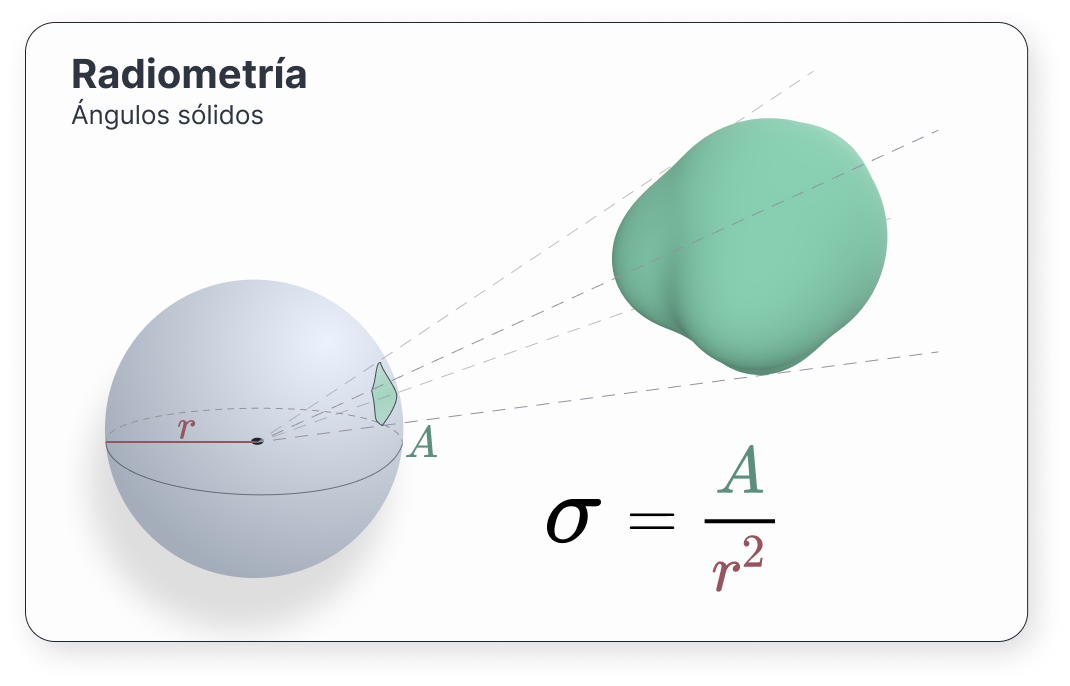
Llevando esta idea a las tres dimensiones es como conseguimos el concepto de ángulo sólido. Si en dos dimensiones teníamos una circunferencia, aquí tendremos una esfera. Cuando generemos las rectas proyectantes hacia el volumen, a diferencia de los ángulos planares, se inscribirá un área en la esfera. La razón entre dicha área \(A\) y el cuadrado del radio \(r\) nos dará un ángulo sólido:
\[ \sigma = \frac{A}{r^2} \text{(sr)} \](9)
Los denotaremos por \(\sigma\), aunque también se pueden encontrar en la literatura como \(\Omega\). Su unidad de medida es el estereorradián (\(\text{sr}\)). Se tiene que \(\sigma \in [0, 4\pi]\). Un esteorradián corresponde a una superficie con área \(r^2\): \(1 \text{sr} = \frac{r^2}{r^2}\).
Usaremos \(\omega\) para representar vectores dirección unitarios en la esfera alrededor de un punto \(p\).
Puesto que estamos trabajando con esferas, nos resultará muy cómodo emplear coordenadas esféricas. Para un cierto punto de coordenadas \((x, y, z)\) de la esfera unitaria, se tiene que
\[ \begin{aligned} \begin{cases} x = \sin\theta\cos\phi \\ y = \sin\theta\sin\phi \\ z = \cos\theta \end{cases} \end{aligned} \](10)
A \(\theta\) se le denomina ángulo polar, mientras que a \(\phi\) se le llama acimut. Imaginémonos un punto en la esfera de radio \(r\) ubicado en una posición \((r, \theta, \phi)\). Queremos calcular un área chiquitita \(dA_h\), de forma que el ángulo sólido asociado a dicha área debe ser \(d\sigma\). Así, \(d\sigma = \frac{dA_h}{r^2}\). Si proyectamos el área, obtenemos \(d\theta\) y \(d\phi\): pequeños cambios en los ángulos que nos generan nuestra pequeña área (“Computer graphics and imaging” 2022, Radiometry & Photometry).
\(dA_h\) debe tener dos lados \(lado_1\) y \(lado_2\). Podemos hallar \(lado_1\) si lo trasladamos al eje \(z\) de nuevo. Así, \(lado_1 = r \sin d\phi\). De la misma manera, \(lado_2 = r d\theta\).
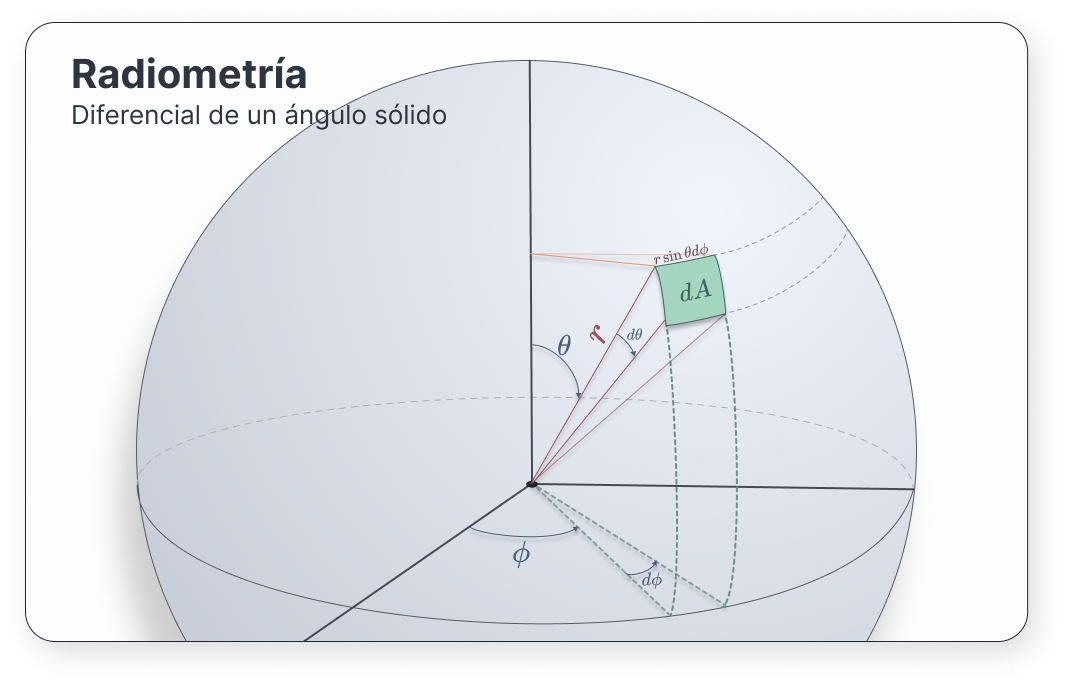
Poniendo estos valores en \(d\sigma\):
\[ \begin{aligned} d\sigma & = \frac{dA_h}{r^2} = \frac{lado_1 lado_2}{r^2} = \\ & = \frac{r \sin\theta\ d\phi\ r\ d\theta}{r^2} = \\ & = \sin\theta\ d\theta\ d\phi \end{aligned} \](11)
¡Genial! Acabamos de añadir un recurso muy potente a nuestro inventario. Esta expresión nos permitirá convertir integrales sobre ángulos sólidos en integrales sobre ángulos esféricos. Por ejemplo, este sería el caso de la esfera.
Supongamos que queremos encontrar el ángulo sólido correspondiente al conjunto de todas las direcciones sobre la esfera \(\mathbb{S}^2\). Se tiene que
\[ \begin{aligned} \sigma & = \int_{\mathbb{S}^2}{d\omega} = \int_{0}^{2\pi} \int_{0}^{\pi} {\sin\theta\ d\theta d\phi} = \\ & = 4\pi \text{ sr} \end{aligned} \]
Además, esto nos dice que un hemisferio de la esfera corresponde a \(2\pi\) estereorradianes.
En la práctica es muy común considerar el ángulo sólido asociado a una dirección en la esfera \(\omega\), el cual se denota por \(d\omega\). A partir de este punto usaremos esa notación.
Los ángulos sólidos nos proporcionan una variedad de herramientas nuevas considerable. Gracias a ellos, podemos desarrollar algunos conceptos nuevos. Uno de ellos es la intensidad radiante.
Imaginémonos un pequeñito punto de luz encerrado en una esfera, el cual emite fotones en todas direcciones (es decir, su ángulo sólido es el de la esfera, \(4\pi\)). Nos gustaría medir cuánta energía pasa por la esfera. Podríamos entonces definir
\[ I = \frac{\Phi}{4\pi} \text{(W/sr)} \]
Si en vez de utilizar toda la esfera, cerramos el ángulo lo máximo posible, nos estaríamos restringiendo a un área extremadamente pequeña, lo cual nos proporcionaría la densidad angular de flujo radiante:
\[ I = \lim_{\Delta\omega \to 0}{\frac{\Delta\Phi}{\Delta\omega}} = \frac{d\Phi}{d\omega} \](12)
De la misma manera que con los conceptos anteriores, podemos volver a la potencia integrando sobre un conjunto de direcciones \(\Omega\) de la esfera:
\[ \Phi = \int_{\Omega}{I(\omega)d\omega} \]
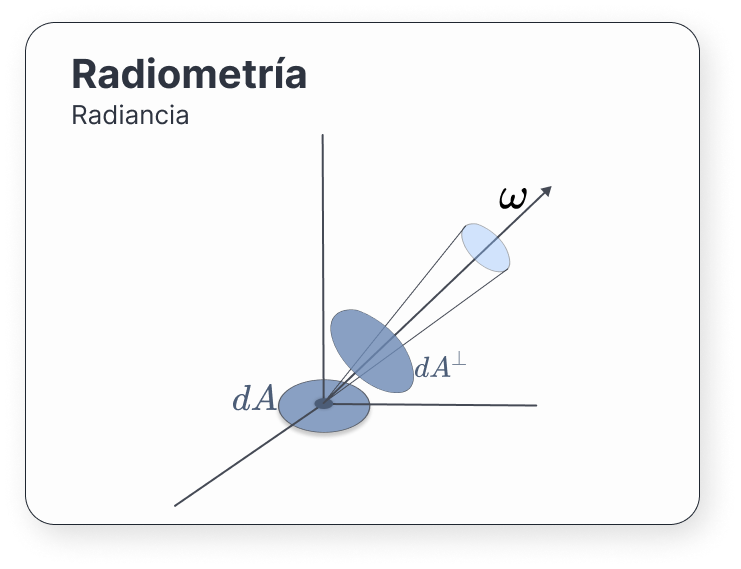
Finalmente, llegamos a uno de los conceptos más importantes de esta sección, el cual es una extensión de la radiancia emitida teniendo en cuenta la dirección de la luz. La radiancia espectral (o radiancia a secas2) (Pharr, Jakob, and Humphreys 2016, Radiometry), denotada por \(L(p, \omega)\), es la irradiancia por unidad de ángulo sólido \(d\omega\) asociado a una dirección \(\omega\):
\[ L(p, \omega) = \lim_{\Delta\omega \to 0}{\frac{\Delta E_\omega(p)}{\Delta\omega}} = \frac{dE_\omega(p)}{d\omega} \](13)
Expandiendo esta expresión, se tiene que la radiancia también es la potencia que pasa por un punto \(p\) y viaja en una dirección \(\omega\) por unidad de área (perpendicular a \(\omega\)) alrededor de \(p\), por unidad de ángulo sólido \(d\omega\):
\[ L(p, \omega) = \frac{d^2\Phi(p, \omega)}{d\omega\ dA^\bot} = \frac{d^2\Phi(p, \omega)}{d\omega\ dA\ \cos\theta} \](14)
donde \(dA^\bot\) es el área proyectada por \(dA\) en una hipotética superficie perpendicular a \(\omega\):
Cuando un rayo impacta en una superficie, \(L\) puede tomar valores muy diferentes en un lado y otro de esta. A fin de cuentas, necesitamos distinguir entre los fotones que llegan a la superficie y los que salen. Para solucionarlo podemos distinguir entre la radiancia que llega a un punto –la incidente–, y la saliente.
A la radiancia incidente o entrante la llamaremos \(L_i(p, \omega)\), mientras que la radiancia saliente se denomina \(L_o(p, \omega)\).
Es importante destacar que \(\omega\) apunta hacia fuera de la superficie. Para \(L_o(p, \omega)\) se tiene que la radiancia viaja en el sentido de \(\omega\), mientras que para \(L_i(p, \omega)\) se tiene que la radiancia viaja en el sentido contrario a \(\omega\); es decir, hacia el punto \(p\).
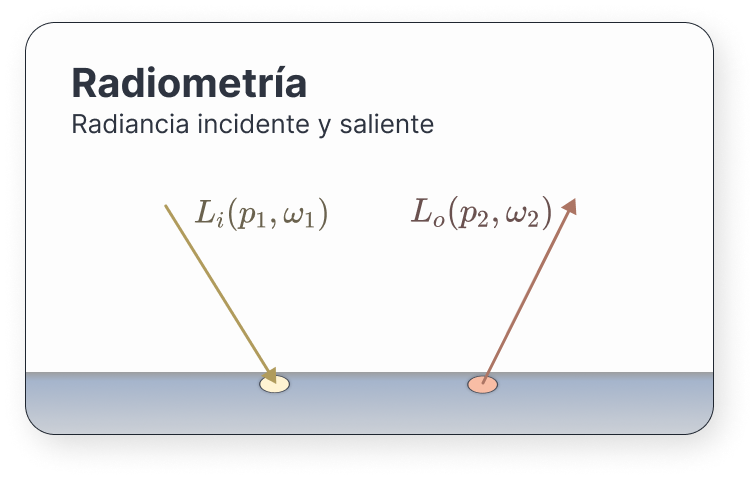
Una propiedad a tener en cuenta es que, si cogemos un punto \(p\) del espacio donde no existe ninguna superifcie, \(L_o(p, \omega) = L_i(p, -\omega) = L(p, \omega)\)
La importancia de la radiancia se debe a un par de propiedades:
La primera de ellas es que, dado \(L\), podemos calcular cualquier otra unidad básica mediante integración. Además, su valor se mantiene constante en rayos que viajan en el vacío en línea recta (Fabio Pellacini 2022). Esto último hace que resulte muy natural usarla en un ray tracer.
Veamos por qué ocurre esto:
Consideremos dos superficies ortogonales entre sí separadas una distancia \(r\). Debido a la conservación de la energía, cualquier fotón que salga de una superficie y se encuentre bajo el ángulo sólido de la otra debe llegar impactar en dicha superficie opuesta.
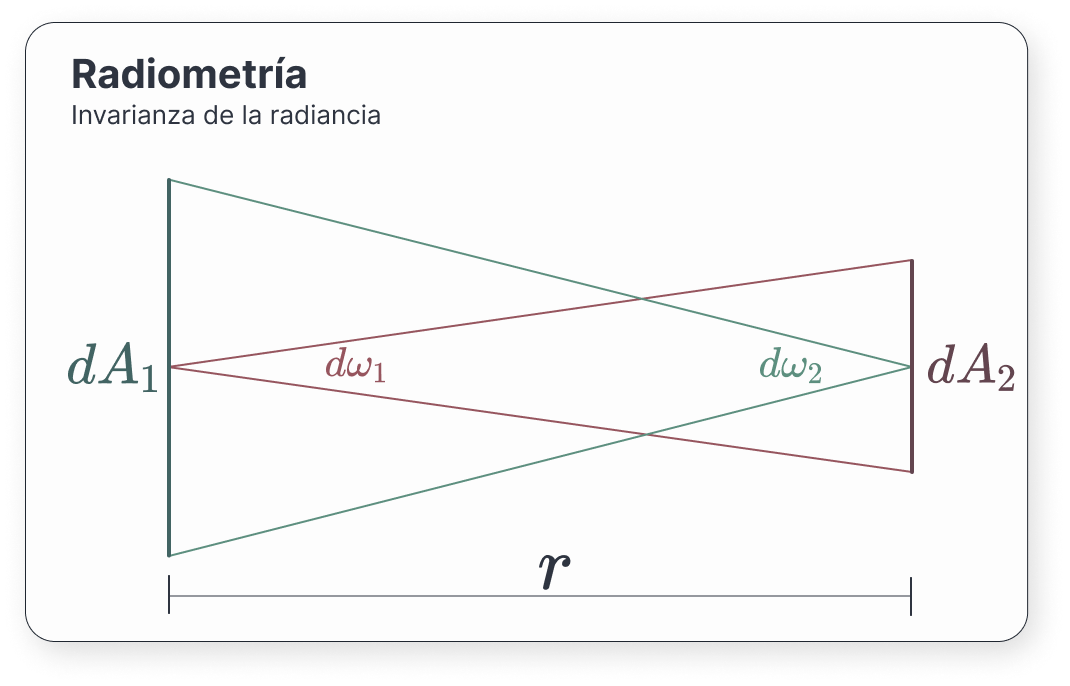
Por tanto:
\[ d^2\Phi_1 = d^2\Phi_2 \]
Sustituyendo en la expresión de la radiancia [14], y teniendo en cuenta que son ortogonales (lo que nos dice que \(\cos\theta = 1\)):
\[ L_1 d\omega_1 dA_1 = L_2 d\omega_2 dA_2 \]
Por construcción, podemos cambiar los ángulos sólidos:
\[ L_1 \frac{dA_2}{r^2} dA_1 = L_2 \frac{dA_1}{r^2} dA_2 \]
Lo que finalmente nos dice que \(L_1 = L_2\), como queríamos ver.
En esta sección, vamos a explorar las nuevas herramientas que nos proporciona la radiancia. Veremos también cómo integrar ángulos sólidos, y cómo simplificar dichas integrales.
Como dijimos al final de la sección de la irradiancia, esta medida no tiene en cuenta las direcciones desde las que llegaba la luz. A diferencia de esta, la radiancia sí que las utiliza. Dado que una de las ventajas de la radiancia es que nos permite obtener el resto de medidas radiométricas, ¿por qué no desarrollamos una nueva expresión de la irradiancia?
Para obtener cuánta luz llega a un punto, debemos acumular la radiancia incidente que nos llega desde cualquier dirección. Dado un punto \(p\) que se encuentra en una superficie con normal \(\mathbf{n}\) en dicho punto, la irradiancia se puede expresar como (Pharr, Jakob, and Humphreys 2016, Working with Radiometric Integrals)
\[ E(p, \mathbf{n}) = \int_{\Omega}{L_i(p, \omega) \left\lvert cos\theta \right\rvert d\omega} \](15)
Siendo \(\Omega\) un subcojunto de direcciones de la esfera \(\mathbb{S}^2\). El término \(\cos\theta\) aparece en la integral debido a la derivada del área proyectada, \(dA^\bot\). \(\theta\) es el ángulo entre la dirección \(\omega\) y la normal \(\mathbf{n}\).
Generalmente, la irradiancia se calcula únicamente en el hemisferio de direcciones asociado a la normal en el punto, \(H^2(\mathbf{n})\).

Podemos eliminar el \(\cos\theta\) de la integral mediante una pequeña transformación: proyectando el ángulo sólido sobre el disco alrededor del punto \(p\) con normal \(\mathbf{n}\), obtenemos una expresión más sencilla: como \(d\omega^\bot = \left\lvert \cos\theta \right\rvert d\omega\), entonces
\[ \begin{aligned} E(p, \mathbf{n}) = \int_{H^2(\mathbf{n})}{L_i(p, \omega) d\omega^\bot} \end{aligned} \]
Usando lo que aprendimos sobre la derivada de los ángulos sólidos [11], se puede reescribir la ecuación anterior como
\[ E(p, \mathbf{n}) = \int_{0}^{2\pi}\int_{0}^{\pi/2}{L_i(p, \theta, \phi) \cos\theta\ \sin\theta\ d\theta\ d\phi} \]
Si integramos esta expresión para todos los puntos de una superficie \(A\), obtenemos la potencia total saliente de esa superficie en todas las direcciones:
\[ \begin{aligned} \Phi & = \int_{A}\int_{H^2(\mathbf{n})}{L_o(p, \omega) \cos\theta\ d\omega dA} = \\ & = \int_{A}\int_{H^2(\mathbf{n})}{L_o(p, \omega) d\omega^\bot dA} \end{aligned} \]
Una herramienta más que nos vendrá bien será la capacidad de convertir integrales sobre direcciones en integrales sobre área. Hemos hecho algo similar en las secciones anteriores, así que no perdemos nada por generalizarlo.
Considera un punto \(p\) sobre una superficie con normal en dicho punto \(\mathbf{n}\). Supongamos que tenemos una pequeña área \(dA\) con normal \(\mathbf{n_{dA}}\). Sea \(\theta\) el ángulo entre \(\mathbf{n}\) y \(\mathbf{n_{dA}}\), y \(r\) la distancia entre \(p\) y \(dA\).
Entonces, la relación entre un ángulo sólido diferencial y un área diferencial es
\[ d\omega = \frac{dA\cos\theta}{r^2} \](16)
Esto nos permite, por ejemplo, expandir algunas expresiones como la de la irradiancia [15] si partimos de un cuadrilátero \(dA\):
\[ \begin{aligned} E(p, \mathbf{n}) & = \int_{\mathbb{S}^2}{L_i(p, \omega) \left\lvert \cos\theta \right\rvert d\omega} = \\ & = \int_{A}{L\cos\theta\ \frac{\cos\theta_o}{r^2}dA} \end{aligned} \]
siendo \(\theta_o\) el ángulo de la radiancia de salida de la superficie del cuadrilátero.
Existe un área de la física muy similar a la radiometría denominada fotometría. La fotometría se encarga de medir la luminosidad percibida, puesto que el ojo humano tiene una sensibilidad específica para cada longitud de onda (Zsolnai-Fehér and Celarek 2022). En vez de radiancia, se suele hablar de luminancia, y todas las unidades vistas durante este capítulo tienen su análogo.
| Radiometría | Símbolo y unidad | Fotometría | Símbolo y unidad |
|---|---|---|---|
| Energía radiante | \(Q_e\), julios \((\text{J})\) | Energía lumínica | \(Q_v\), lumen segundo \((\text{lm s})\) |
| Flujo radiante | \(\phi_e\), vatios \((\text{W})\) | Flujo luminoso | \(\phi_v\), lumen \((\text{lm} = \text{cd sr})\) |
| Intensidad radiante | \(I_e\), vatios por estereorradián \((\text{W/sr})\) | Intensidad luminosa | \(I_v\), candela \((\text{cd} = \text{lm/sr})\) |
| Radiancia | \(L_e\), \((\text{W sr}^{-1}\text{m}^{-1})\) | Luminancia | \(L_v\), candela por metro cuadrado \((\text{cd/m}^{2})\) |
| Irradiancia | \(E_e\), \((\text{W/m}^{2})\) | Iluminancia | \(E_v\), lux \((\text{lx} = \text{lm/m}^2)\) |
Cuando la luz impacta en una superficie, ocurren un par de sucesos: parte de los fotones se reflejan saliendo disparados hacia alguna dirección, mientras que otros se absorben. La forma en la que se comportan depende de cómo sea la superficie. Específicamente, del material del que esté hecha.
En informática gráfica se consideran tres tipos principales de dispersión de luz: dispersión y reflexión en superficies (surface scattering), dispersión volumétrica (volumetric scattering) y dispersión bajo superficie (subsurface scattering)
En este capítulo vamos a modelar la primera. Estudiaremos qué es lo que ocurre cuando los fotones alcanzan una superficie, en qué dirección se reflejan, y cómo cambia el comportamiento dependiendo de las propiedades del material.
La función de distribución de reflectancia bidireccional (en inglés, bidirectional reflectance distribution function, BRDF) (Pharr, Jakob, and Humphreys 2016, Surface Reflection) describe cómo la luz se refleja en una superficie opaca. Se encarga de informarnos sobre cuánta radiancia sale en dirección \(\omega_o\) debido a la radiancia incidente desde la dirección \(\omega_i\), partiendo de un punto \(p\) en una superficie con normal \(\mathbf{n}\). Depende de la longitud de onda \(\lambda\), pero, como de costumbre, la omitiremos.
Intuición: ¿cuál es la probabilidad de que, habiéndome llegado un fotón desde \(\omega_i\), me salga disparado hacia \(\omega_o\)?
Si consideramos \(\omega_i\) como un cono diferencial de direcciones, la irradiancia diferencial en \(p\) viene dada por
\[ dE(p, \omega_i) = L_i(p, \omega_i) \cos\theta_i\ d\omega_i \]
Debido a esta irradiancia, una pequeña parte de radiancia saldrá en dirección \(\omega_o\), proporcional a la irradiancia:
\[ dL_o(p, \omega_o) \propto dE(p, \omega_i) \]
Si lo ponemos en forma de cociente, sabremos exactamente cuál es la proporción de luz. A este cociente lo llamaremos \(f_r(p, \omega_o \leftarrow \omega_i)\); la función de distribución de reflectancia bidireccional:
\[ f_r(p, \omega_o \leftarrow \omega_i) = \frac{dL_o(p, \omega_o)}{dE(p, \omega_i)} = \frac{dL_o(p, \omega_o)}{L_i(p, \omega_i) \cos\theta_i\ d\omega_i} (\text{sr}^{-1}) \]
Nota(ción): dependiendo de la fuente que estés leyendo, es posible que te encuentres una integral algo diferente. Por ejemplo, en (Shirley and Morley 2003) se integra con respecto a los ángulos de salida \(\omega_o\), en vez de los incidentes.
Aquí, usaremos la notación de integrar con respecto a los incidentes, como se hace en (Pharr, Jakob, and Humphreys 2016).
Las BRDF físicamente realistas tienen un par de propiedades importantes:
\[ \int_{H^2(\mathbf{n})}{f_r(p, \omega_o \leftarrow \omega_i) \cos\theta_i\ d\omega_i} \leq 1 \]
Si la BRDF describe cómo se refleja la luz, la bidirectional transmittance distribution function (abreviada BTDF) nos informará sobre la transmitancia; es decir, cómo se comporta la luz cuando entra en un medio. Generalmente serán dos caras de la misma moneda: cuando la luz impacta en una superficie, parte de ella, se reflejará, y otra parte se transmitirá.
Puedes imaginarte la BTDF como una función de reflectancia del hemisferio opuesto a donde se encuentra la normal de la superficie.
Denotaremos a la BTDF por
\[ f_t(p, \omega_o \leftarrow \omega_i) \]
Al contrario que en la BRDF, \(\omega_o\) y \(\omega_i\) se encuentran en hemisferios diferentes.
Convenientemente, podemos unir la BRDF y la BTDF en una sola expresión, llamada la función de distribución de dispersión bidireccional (bidirectional scattering distribution function, BSDF). A la BSDF la denotaremos por
\[ f(p, \omega_o \leftarrow \omega_i) \]
Nota(ción): también se suele utilizar BxDF en vez de BSDF.
Usando esta definición, podemos obtener
\[ dL_o(p, \omega_o) = f(p, \omega_o \leftarrow \omega_i) L_i(p, \omega_i) \left\lvert \cos\theta_i \right\rvert d\omega_i \]
Esto nos deja a punto de caramelo una nueva expresión de la randiancia en términos de la randiancia incidente en un punto \(p\). Integrando la expresión anterior, obtenemos
\[ L_o(p, \omega_o) = \int_{\mathbb{S}^2}{f(p, \omega_o \leftarrow \omega_i)L_i(p, \omega_i)\left\lvert \cos\theta_i \right\rvert d\omega_i} \](17)
siendo \(\mathbb{S}^2\) la esfera.
Intuición: la BSDF son todas las posibles direcciones en las que puede salir disparada la luz.
Esta forma de expresar la radiancia es muy importante. Generalmente se le suele llamar la ecuación de dispersión (scattering equation, en inglés), y en capítulos posteriores buscaremos formas de evaluarla rápidamente. ¡Los métodos de Monte Carlo nos vendrán de perlas!
Las BSDFs tienen unas propiedades interesantes:
\[ \int_{H^2(\mathbf{n})}{f(p, \omega_o \leftarrow \omega_i) \cos\theta_i\ d\omega_i} \le 1\ \forall \omega_o \]
Puede ser útil tomar el comportamiento agregado de las BRDFs y las BTDFs y reducirlo un cierto valor que describa su comportamiento general de dispersión. Sería algo así como un resumen de su distribución. Para conseguirlo, vamos a introducir dos nuevas funciones:
El albedo (Szirmay-Kalos 2000), también conocido como la reflectancia hemisférica-direccional (hemispherical-directional reflectance) (Pharr, Jakob, and Humphreys 2016, Reflection Models, Basic Interface) describe la radiancia saliente en la dirección \(\omega_o\), supuesto que la radiancia entrante desde cualquier dirección es constante e igual a la unidad:
\[ \rho_{hd}(\omega_o) = \int_{H^2(n)}{f_r(p, \omega_o \leftarrow \omega_i) \left\lvert \cos\theta_i \right\rvert\ d\omega_i} \]
Por otra parte, la reflectancia hemisférica-hemisférica (hemispherical-hemispherical reflectance) es un valor espectral que nos proporciona el ratio de luz incidente reflejada por una superficie, suponiendo que llega la misma luz desde todas direcciones:
\[ \rho_{hh} = \frac{1}{\pi} \int_{H^2(n)} \int_{H^2(n)}{f_r(p, \omega_o \leftarrow \omega_i) \left\lvert \cos\theta_o\ \cos\theta_i \right\rvert\ d\omega_o\ d\omega_i} \]
En la práctica, cada superficie tendrá una BSDF característica. Esto hace que la luz adquiera una dirección particular al incidir en cada punto de esta. En esta sección, vamos a tratar algunas BSDFs particulares e introduciremos las fórmulas fundamentales que se usan en los modelos de materiales (también conocidos como modelos de shading).
Los tipos de materiales que trataremos son los más básicos. Entre ellos, se encuentran los difusos lambertianos, materiales dieléctricos, espejos y algunas BSDFs compuestas. Un repertorio de implementaciones se encuentra en el repositorio de BRDFs de Walt Disney Animation Studios (“BRDF explorer” 2019).
Prácticamente toda superficie, en mayor o menor medida, refleja parte de la luz incidente. Otros tipos de materiales reflejan y refractan a la vez, como puede ser un espejo o el agua.
En esencia, los reflejos se pueden clasificar en cuatro grandes tipos (McGuire 2021, Materials):
Ten en cuenta que es muy difícil encontrar objetos físicos que imiten a la perfección un cierto modelo. Suelen recaer en un híbrido entre dos o más modelos.
Fijado un cierto modelo, la función de distribución de reflectancia, BRDF, puede ser isotrópica o anisotrópica. Los materiales isotrópicos son aquellos cuya BRDF \(f_r(p, \omega_o \leftarrow \omega_i)\) no cambia cuando se rotan los vectores \(\omega_o, \omega_i\) un mismo ángulo alrededor de \(p\). La mayor parte de los materiales son de este tipo.
Por el contrario, si la BRDF sí cambia cuando se aplica dicha rotación, entonces nos encontramos ante un material anisotrópico. Esto suele ocurrir cuando tratamos con superficies pulidas con surcos. Algunos ejemplos son los discos de vinilo y los metales pulidos en una dirección.
Primero, tratemos con materiales que únicamente reflejan luz; es decir, su BSDF es una BRDF.
Para un material especular perfecto (es decir, espejos), la dirección reflejada \(\omega_o\) dado un rayo incidente \(\omega_i\) es (Haines 2021, 105; Pharr, Jakob, and Humphreys 2016, Specular Reflection and Transmission; McGuire 2021, Materials):
\[ \omega_o = 2 \mathbf{n} (\omega_i \cdot \mathbf{n}) -\omega_i \]
siendo \(\mathbf{n}\) la normal en el punto incidente. Con esta expresión, se necesita que \(\mathbf{n}\) esté normalizado. Para los otros dos vectores no es necesario; la dirección de salida tendrá la misma norma que la de entrada.
La BRDF de un material especular perfecto se describe en términos de la proporción de radiancia reflejada hacia \(\omega_o\) dependiente del vector incidente \(\omega_i\), la cual puede viene descrita por \(\rho_{hd}(\omega_i)\). Se da la relación
\[ \rho_{hd}(\omega_i) = \int_{\mathbb{S}^2} {f_r(p, \omega_o \leftarrow \omega_i)\ d\omega_o} \]
Puesto que en los espejos perfectos no se pierde energía, necesariamente \(\rho_{hd} = 1\).
Debemos tener en cuenta que la probabilidad de que un rayo tenga una dirección diferente a la del reflejo es 0, por lo que
\[ f_r(p, \omega_o \leftarrow \omega_i) = 0 \qquad \forall\ \omega_0 \ne 2 \mathbf{n} (\omega_i \cdot \mathbf{n}) -\omega_i \]
La función de densidad evaluada en el vector reflejado es problemática. Está claro que debe integrar \(\rho_{hd}\), pero el ángulo sólido en el que se integra tiene medida cero, pues toda la radiancia se refleja hacia una única dirección. Esto significa que
\[ f_r(\omega_o \leftarrow \omega_i ) = \frac{\rho_{hd}(\omega_i)}{0 \left\lvert \omega_i \cdot \mathbf{n} \right\rvert} \]
Podemos solucionar este problema utilizando una Delta de Dirac, obteniendo finalmente la BRDF de los materiales especulares perfectos:
\[ \begin{aligned} f_r(\omega_o \leftarrow \omega_i ) & = \frac{\delta(\omega_o, \omega_i) \rho_{hd}(\omega_i)}{\left\lvert \omega_i \cdot \mathbf{n} \right\rvert} = \\ & = \frac{\delta(\omega_o, \omega_i) \left\lvert \omega_i \cdot \mathbf{n} \right\rvert k_r}{\left\lvert \omega_i \cdot \mathbf{n} \right\rvert} \end{aligned} \](18)
siendo \(\rho_{hd}(\omega_i) = \left\lvert \omega_i \cdot \mathbf{n} \right\rvert k_r\) el albedo, con \(k_r\) el coeficiente de reflectividad, cuyo valor se encuentra entre 0 y 1, dependiendo de la energía que se pierda.
Este es uno de los modelos más sencillos. Es conocido también como el modelo lambertiano. Se asume que la superficie es completamente difusa, lo cual implica que la luz se refleja en todas direcciones equiprobablemente, independientemente del punto de vista del observador (McGuire 2021, Materials). Esto significa que
\[ f_r(\omega_o \leftarrow \omega_i) = \frac{\rho_{hd}}{\pi} \]
El albedo \(0 \le \rho_{hd} \le 1\) es la reflectividad de la superficie. El denominador es aquel coeficiente tal que se normalice la BRDF:
\[ \int_{\mathbb{S}^2} {\max(\mathbf{n} \cdot \omega_i, 0)\ d\omega_i} = \pi \]
En la práctica no se utiliza mucho, pues está muy limitado.
El modelo de Phong se basa en la observación de que, cuando el punto de vista se alinea con la dirección del vector de luz reflejado, aparecen puntos muy iluminados, lo que se conoce como resaltado especular.
Su BRDF es
\[ f_r(p, \omega_o \leftarrow \omega_i) = \frac{\alpha + 2}{2\pi} \max{(0, \omega_i \cdot \omega_o)}^\alpha \]
donde \(\alpha\) es índice del brillo del material, y \(\omega_o\) el vector reflejado teniendo en cuenta \(\omega_i\) y \(\mathbf{n}\). El coeficiente \(\frac{\alpha + 2}{2\pi}\) se utiliza para normalizarla (Giesen 2009)
Este modelo de iluminación se suele usar en rasterización y no es común encontrarlo en ray tracing físicamente realista. En su versión de rasterización hace falta definir los coeficientes ambientales y difusos. Aquí solo hemos optado por el especular.
Este es una pequeña modificación al de Phong. En vez de usar el vector reflejado de luz, se define un vector unitario entre el observador y la luz, \(\mathbf{h} = \frac{\omega + \mathbf{l}}{\left\lVert \omega + \mathbf{l} \right\rVert}\). Resulta más fácil calcularlo. Además, este modelo es más realista.
\[ f_r(p, \omega_o \leftarrow \omega_i) = \frac{8 \pi(2^{-\alpha/2} + \alpha)}{(\alpha + 2)(\alpha + 4)} \max\{0, \mathbf{h} \cdot \mathbf{n}\}^\alpha \]
De la misma manera que en Phong, \(\frac{8 \pi(2^{-\alpha/2} + \alpha)}{(\alpha + 2)(\alpha + 4)}\) es el coeficiente de normalización de la BRDF (Giesen 2009).
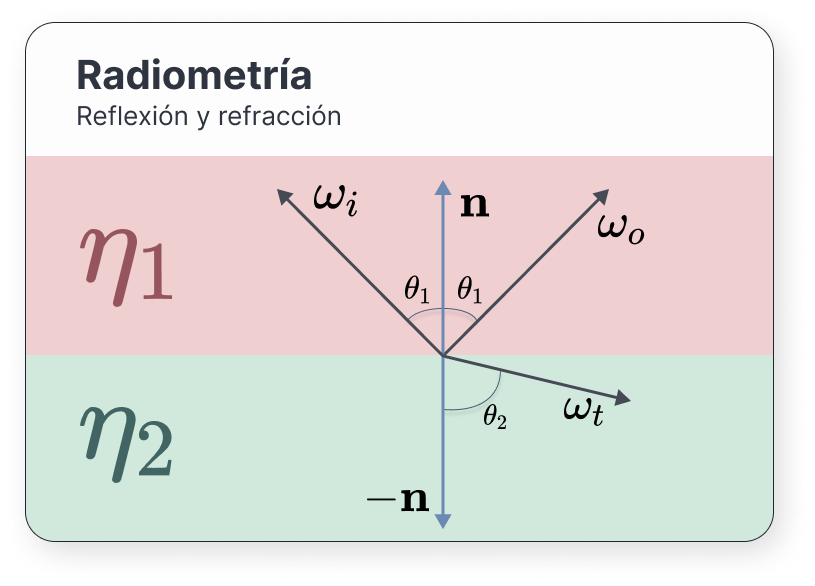
Algunos materiales permiten que la luz los atraviese –conocido como transmisión–. En estos casos, decimos que se produce un cambio en el medio. Para conocer cómo de rápido viajan los fotones a través de ellos, se utiliza un valor denominado índice de refracción, usualmente denotado por \(\eta\):
\[ \eta = \frac{c}{\nu} \]
siendo \(c\) la velocidad de la luz en el vacío y \(\nu\) la velocidad de fase del medio, la cual depende de la longitud de onda. Sin embargo, como hemos comentado varias veces, no tendremos en cuenta la longitud de onda en nuestro ray tracer, por lo que no nos tenemos que preocupar de esto.
Algunos materiales como el aire tienen un índice de refracción \(\eta_{\text{aire}} = 1.0003\), mientras que el del agua vale \(\eta_{\text{agua}} = 1.333\), y el del cristal vale \(\eta_{\text{cristal}} = 1.52\).
La ley de Snell nos proporciona una ecuación muy sencilla que relaciona el cambio de un medio con índice de refracción \(\eta_1\) a otro con índice de refracción \(\eta_2\):
\[ \eta_1 \sin\theta_1 = \eta_2 \sin\theta_2 \](19)
siendo \(\theta_1\) y \(\theta_2\) los ángulos de entrada y salida respectivamente.
Usualmente, los índices de refración son conocidos, así como el ángulo de incidencia \(\theta_1\), por lo que podremos calcular el ángulo del vector refractado con facilidad:
\[ \theta_2 = \arcsin{\left(\frac{\eta_1}{\eta_2}\sin\theta_2\right)} \]
Cuando cambiamos de un medio con índice de refracción \(\eta_1\) a otro con \(\eta_2 < \eta_1\), podemos encontrarnos ante un caso de reflexión interna total. Analíticamente, lo que ocurre es que
\[ \sin\theta_2 = \frac{\eta_1}{\eta_2}\sin\theta_1 > 1 \]
lo cual no puede ocurrir. Se denomina el ángulo crítico a aquel \(\theta_1\) para la cual \(\frac{\eta_1}{\eta_2}\sin\theta_1 > 1\):
\[ \theta_1 = \arcsin{\left(\frac{\eta_2}{\eta_1}\right)} \]
Por ejemplo, si un haz de luz viaja desde un cristal hacia un cuerpo de agua, entonces \(\theta_1 = \arcsin{(1.333/1.52)} \approx 1.06\) radianes \(= 61.04\textdegree\).
Lo que ocurre en estos casos es que, en vez de pasar al segundo medio, los fotones vuelven al primero; creando un reflejo como si de un espejo se tratara.

El vector refractado \(\omega_t\) puede conseguirse a partir de la siguiente expresión (McGuire 2021):
\[ \omega_t = - \frac{\eta_1}{\eta_2}\left(\omega_i - (\omega_i \cdot \mathbf{n})\mathbf{n}\right) - \left( \sqrt{1 - \left(\frac{\eta_1}{\eta_2}\right)^2 \left(1 - (\omega_i \cdot \mathbf{n}^2)\right)} \right) \cdot \mathbf{n} \]
Aquellos materiales que refractan y reflejan luz (como el agua de la foto anterior) no pueden generar energía de la nada; por lo que la combinación de ambos efectos debe ser proporcional a la luz incidente. Es decir, una fracción de luz es reflejada, y otra es refractada. Las ecuaciones de Fresnel nos permiten conocer esta cantidad.
La proporción de luz reflejada desde un rayo que viaja por un medio con índice de refracción \(\eta_1\) y ángulo de incidencia \(\theta_1\) a otro medio con índice de refracción \(\eta_2\) es (Majercik 2021, 109):
\[ \begin{aligned} R_s & = \left\lvert \frac {\eta_1 \cos\theta_1 - \eta_2 \sqrt{1 - \left( \frac{\eta_1}{\eta_2}\sin\theta_1\right) ^2}} {\eta_1 \cos\theta_1 + \eta_2 \sqrt{1 - \left( \frac{\eta_1}{\eta_2}\sin\theta_1\right) ^2}} \right\rvert^2 \\ R_p & = \left\lvert \frac {\eta_1 \sqrt{1 - \left( \frac{\eta_1}{\eta_2}\sin\theta_1\right)^2} - \eta_2\cos\theta_1} {\eta_1 \sqrt{1 - \left( \frac{\eta_1}{\eta_2}\sin\theta_1\right)^2} + \eta_2\cos\theta_1} \right\rvert^2 \end{aligned} \](20)
donde los subíndices \(s\) y \(p\) denotan la polarización de la luz: \(s\) es perpendicular a la dirección de propagación, mientras que \(p\) es paralela.
Generalmente en los ray tracers se simula luz no polarizada, así que se deben promediar ambos valores. Por lo tanto, se debe usar el valor \(R\) definido de la siguiente manera:
\[ R = \frac{R_s + R_p}{2} \](21)
Como podemos imaginarnos, calcular las expresiones de Fresnel [20] no es precisamente barato. En la práctica, todo el mundo utiliza una aproximación creada por Schlick, la cual funciona sorprendentemente bien. Viene dada por
\[ R(\theta_1) = R_0 + (1 - R_0)(1 - \cos\theta_1)^5 \](22)
siendo \(R_0 = R(0)\); es decir, el valor que toma \(R\) cuando el rayo incidente es paralelo al medio. Su valor es
\[ R_0 = \left(\frac{\eta_1 - \eta_2}{\eta_1 + \eta_2}\right)^2 \]
Esta aproximación es 32 veces más rápida de calcular que las ecuaciones de Fresnel, generando un error medio inferior al 1% (Schlick 1994)
La mayor parte de las superficies no son puramente lisas a nivel microscópico. En la mayoría de materiales existen microfacetas, las cuales producen que la luz no se refleje de forma especular. Esto hace que la luz pueda salir en direcciones muy diferentes dependiendo de la rugosidad de la superficie. Este tipo de materiales suele necesitar una función que caracterice la distribución de las normales de las microfacetas (denotada por \(\mathbf{n_f}\)).
Un modelo que utiliza esta idea es el de Oren-Nayar, el cual describe la reflexión difusa de una superficie. Se basa en la idea de que las superficies rugosas aparentan ser más brillantes conforme la dirección de la luz se aproxima a la dirección de la vista. La BRDF de Oren-Nayar es (Pharr, Jakob, and Humphreys 2016, Microfacet Models)
\[ f_r(p, \omega_o \leftarrow \omega_i) = \frac{\rho}{\pi} \left(A + B\max{(0, \cos(\phi_i - \phi_o))}\sin\alpha\tan\beta\right) \]
donde, si \(\theta\) está en radianes,
\[ \begin{aligned} A & = 1 - \frac{\theta^2}{2(\theta^2 + 0.33)} \\ B & = \frac{0.45 \theta^2}{\theta^2 + 0.09} \\ \alpha & = \max{(\theta_i, \theta_o)} \\ \beta & = \min{(\theta_i, \theta_o)} \end{aligned} \]
En la actualidad, el modelo más utilizado de microfacetas es el GGX. Motores modernos como Unreal Engine 4 y Unity lo utilizan en sus pipelines físicamente realistas. La BRDF se define de la siguiente manera (McGuire 2021):
\[ \begin{aligned} f_r(p, \omega_o, \omega_i) & = \frac { D(p, \omega_h) F(p, \omega_i, \omega_o) G_{1}(p, \omega_i, \omega_h) G_{1}(p, \omega_o, \omega_h) } { 4\pi (\mathbf{n} \cdot \omega_i) (\mathbf{n} \cdot \omega_o) } = \\ & = \frac { 4 \alpha^2_p \left(F_0 + (1 - F_0)(1 - \max{(0, \omega_h \cdot \omega_i})^5\right)(\mathbf{n} \cdot \omega_i)(\mathbf{n} \cdot \omega_o) } { \pi \left(1 + (\alpha^2_p - 1) \cdot (\mathbf{n} \cdot \omega_h)^2\right)^2 A_1 A_2 } \end{aligned} \]
siendo
\[ \begin{aligned} A_1 & = \left((\mathbf{n} \cdot \omega_i) + \sqrt{\alpha^2_p + (1 - \alpha^2_p)(\mathbf{n} \cdot \omega_i)^2}\right) \\ A_2 & = \left((\mathbf{n} \cdot \omega_o) + \sqrt{\alpha^2_p + (1 - \alpha^2_p)(\mathbf{n} \cdot \omega_o)^2}\right) \end{aligned} \]
y donde
Y, finalmente, tras esta introducción de los principales conceptos radiométricos, llegamos a la ecuación más importante de todo este trabajo: la rendering equation; también llamada la ecuación del transporte de luz.
Antes de comenzar, volvamos a plantear de nuevo la situación: nos encontramos observando desde nuestra pantalla una escena virtual mediante la cámara. Queremos saber qué color tomará un pixel específico. Para conseguirlo, dispararemos rayos desde nuestro punto de vista hacia el entorno, haciendo que reboten en los objetos. Cuando un rayo impacte en una superficie, adquirirá parte de las propiedades del material del objeto. Además, de este rayo surgirán otros nuevos (un rayo dispersado y otro refractado), que a su vez repetirán el proceso. La información que se obtiene a partir de estos caminos de rayos nos permitirá darle color al píxel. Con dicha ecuación, describiremos analíticamente cómo ocurre esto.
Un último concepto más: denotemos por \(L_e(p, \omega_o)\) a la radiancia producida por los materiales emisivos. En esencia, estos materiales son fuentes de luz, pues emiten radiancia por sí mismos.
La rendering equation viene dada por la siguiente expresión:
\[ L_o(p, \omega_o) = L_e(p, \omega_o) + \int_{H^2(\mathbf{n})}{f(p, \omega_o \leftarrow \omega_i) L_i(p, \omega_i) \cos\theta_i\ d\omega_i} \](23)
Esta ecuación nos proporciona una forma de calcular la radiancia total saliente \(L_o\) en un punto. Esta puede ser hallada como la suma de la radiancia producida por la superficie en dicho punto, \(L_e\) y la radiancia reflejada por el entorno, a la que llamaremos \(L_r\).
\[ L_r(p, \omega_o) = \int_{H^2(\mathbf{n})}{f(p, \omega_o \leftarrow \omega_i) L_i(p, \omega_i) \cos\theta_i\ d\omega_i} \](24)
Esta radiancia reflejada se calcula integrando \(f(p, \omega_o \leftarrow \omega_i) L_i(p, \omega_i) \cos\theta_i\) sobre todas las posibles direcciones de luz. Este integrando viene dado por la BSDF \(f(p, \omega_o \leftarrow \omega_i)\), que describe el comportamiento del material en el punto \(p\); la radiancia incidente \(L_i\) en dicho punto; y el ángulo de incidencia \(\theta_i\) de la dirección de entrada con respecto a la normal.
En la ecuación [23], si el material no emite luz, entonces \(L_e = 0\); y la radiancia total de salida coincide con la radiancia total reflejada [24].
Para hacerla operativa en términos computacionales podemos transformarla un poco. Bien, partamos de la ecuación de para la radiancia reflejada:
Buscamos expresar la radiancia incidente en términos de la radiancia reflejada. Para ello, usamos la propiedad de que la radiancia a lo largo de un rayo no cambia.
Si a una superficie le llega un fotón desde alguna parte, debe ser porque “alguien” ha tenido que emitirlo. El fotón necesariamente ha llegado a partir de un rayo. La propiedad nos dice que la radiancia no ha podido cambiar en el camino.
Pues bien, consideremos una función \(r: \mathbb{R}^3 \times \Omega \to \mathbb{R}^3\) tal que, dado un punto \(p\) y una dirección \(\omega\), devuelve el siguiente punto de impacto en una superficie. En esencia, es una función de ray casting (Fabio Pellacini 2022, Path Tracing).
Esta función nos permite expresar el punto anterior de la siguiente forma:
\[ L_i(p, \omega) = L_o(r(p, \omega), -\omega) \]
Esto nos permite cambiar la expresión de \(L_i\) en la integral anterior:
\[ L_r(p, \omega_o) = \int_{H^2(\mathbf{n})}{f(p, \omega_o \leftarrow \omega_i) L_o(r(p, \omega_i), -\omega_i) \cos\theta_i\ d\omega_i} \]
Finalmente, la radiancia total vendrá dada por la suma de la radiancia emitida y la reflejada:
\[ L_o(p, \omega_o) = L_e(p, \omega_o) + \int_{H^2(\mathbf{n})}{f(p, \omega_o \leftarrow \omega_i) L_o(r(p, \omega_i), -\omega_i) \cos\theta_i\ d\omega_i} \](25)
Y con esto, hemos obtenido una expresión de la rendering equation únicamente en términos de la radiancia de salida.
Si quieres ver gráficamente cómo funciona, te recomiendo pasarte por (Arnebäck 2019). Es un vídeo muy intuitivo.
Si nos paramos a pensar, la ecuación [25] es muy similar a la primera [23]. Sin embargo, hay un par de matices que las hacen muy diferentes:
Este último matiz es importante. Para renderizar una imagen, se necesita calcular la radiancia de salida para aquellos puntos visibles desde nuestra cámara.
Como vimos en el capítulo anterior, la clave para conseguir una imagen en nuestro ray tracer es calcular la cantidad de luz en un punto de la escena. Para ello, necesitamos hallar la radiancia en dicha posición mediante la rendering equation. Sin embargo, es muy difícil resolverla; tanto computacional como analíticamente. Por ello, debemos atacar el problema desde otro punto de vista.
En este capítulo veremos los fundamentos de la integración de Monte Carlo, cómo muestrear distribuciones específicas y métodos para afinar el resultado final. Estas técnicas nos permitirán aproximar el valor que toman las integrales mediante una estimación. Utilizando muestreo aleatorio para evaluar puntos de una función, seremos capaces de obtener un resultado suficientemente bueno.
Una de las propiedades que hacen interesantes a este tipo de métodos es la independencia del ratio de convergencia y la dimensionalidad del integrando. Sin embargo, conseguir un mejor rendimiento tiene un precio a pagar. Dadas \(n\) muestras, la convergencia a la solución correcta tiene un orden de \(\mathcal{O}\left(n^{-1/2}\right) = \mathcal{O}\left(\frac{1}{\sqrt{n}}\right)\). Es decir, para reducir el error a la mitad, necesitaríamos 4 veces más muestras. Esto hará que busquemos otras formas de reducir la varianza del estimador.
Antes de comenzar a fondo, necesitaremos unas nociones de variable aleatoria para poder entender la integración de Monte Carlo, por lo que vamos a hacer un breve repaso.
Una variable aleatoria \(X\) (v.a.) es, esencialmente, una regla que asigna un valor numérico a cada posibilidad de un proceso de azar. Formalmente, es una función definida en un espacio de probabilidad \((\Omega, \mathcal{A}, P)\) asociado a un experimento aleatorio:
\[ X: \Omega \rightarrow \mathbb{R} \]
A \(\Omega\) lo conocemos como espacio muestral (conjunto de todas las posibilidades), \(\mathcal{A}\) es una \(\sigma\)-álgebra de subconjuntos de \(\Omega\) que refleja todas las posibilidades de eventos aleatorios, y \(P\) es una función probabilidad, que asigna a cada evento una probabilidad.
Una variable aleatoria \(X\) puede clasificarse atendiendo a cómo sea su rango \(R_X = \left\{x \in \mathbb{R} \,\middle|\, \exists \omega \in \Omega \text{ tal que } X(\omega) = x \right\}\): en discreta o continua, dependiendo de si \(X\) toma valores en un conjunto numerable o no numerable.
Las v.a. discretas son aquellas cuyo rango es un conjunto discreto.
Para comprender mejor cómo funcionan, pongamos un ejemplo: Consideremos un experimento en el que lanzamos dos dados, anotando lo que sale en cada uno. Los posibles valores que toman serán (Galvin n.d.):
\[ \begin{aligned} \Omega = \{ & (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), \\ & (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), \\ & (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), \\ & (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), \\ & (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), \\ & (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) \} \end{aligned} \]
Cada resultado tiene la misma probabilidad de ocurrir (claro está, si el dado no está trucado). Como hay \(36\) posibilidades, la probabilidad de obtener un cierto valor es de \(\frac{1}{36}\).
La v.a. \(X\) denotará la suma de los valores obtenidos en cada uno. Así, por ejemplo, si al lanzar los dados hemos obtenido \((1, 3)\), \(X\) tomará el valor \(4\). En total, \(X\) puede tomar todos los valores comprendidos entre \(2\) y \(12\). Cada pareja no está asociada a un único valor de \(X\). Por ejemplo, \((1, 2)\) suma lo mismo que \((2, 1)\). Esto nos lleva a preguntarnos… ¿Cuál es la probabilidad de que \(X\) adquiera un cierto valor?
La función masa de probabilidad nos permite conocer la probabilidad de que \(X\) tome un cierto valor \(x\). Se denota por \(P\left[ X = x \right]\).
También se suele usar \(p_X(x)\) o, directamente \(p(x)\), cuando no haya lugar a dudas. Sin embargo, en este trabajo reservaremos este nombre a otro tipo de funciones.
Nota(ción): Cuando \(X\) tenga una cierta función masa de probabilidad, escribiremos \(X \sim p_X\)
En este ejemplo, la probabilidad de que \(X\) tome el valor \(4\) es
\[ \begin{aligned} P\left[ X = 4 \right] & = \sum{\small{\text{nº parejas que suman 4}} \cdot \small{\text{probabilidad de que salga la pareja}}} \\ & = 3 \cdot \frac{1}{36} = \frac{1}{12} \end{aligned} \]
Las parejas serían \((1, 3), (2, 2)\) y \((3, 1)\).
Por definición, si el conjunto de valores que puede tomar \(X\) es \(\{x_1, \dots, x_n\}\), la función masa de probabilidad debe cumplir que
\[ \sum_{i = 1}^{n}{P\left[ X = x_i \right]} = 1 \]
Siendo \(P\left[ X = x_i \right] \ge 0\), pues la f.m.p. es no negativa.
Muchas veces nos interesará conocer la probabilidad de que \(X\) se quede por debajo o igual que un cierto valor \(x\) (de hecho, podemos caracterizar distribuciones aleatorias gracias a esto). Para ello, usamos la función de distribución:
\[ F_X(x) = P\left[ X \le x \right] = \sum_{\substack{k \in \mathbb{R} \\ k \le x}}{P\left[ X = k \right]} \]
Es una función continua por la derecha y monótona no decreciente. Además, se cumple que \(0 \le F_X(x) \le 1\) y \(\lim_{x \to -\infty}{F_X} = 0\), \(\lim_{x \to \infty}{F_X} = 1\).
En nuestro ejemplo, si consideramos \(x = 3\):
\[ \begin{aligned} F_X(x) & = \sum_{i = 1}^{3}{P\left[ X = i \right]} = P\left[ X = 1 \right] + P\left[ X = 2 \right] + P\left[ X = 3 \right] \\ & = \frac{1}{36} + \frac{2}{36} + \frac{3}{36} = \frac{1}{12} \end{aligned} \]
Este tipo de variables aleatorias tienen un rango no numerable; es decir, el conjunto de valores que puede tomar abarca un intervalo de números.
Un ejemplo podría ser la altura de una persona.
Si en las variables aleatorias discretas teníamos funciones masa de probabilidad, aquí definiremos las funciones de densidad de probabilidad (o simplemente, funciones de densidad). La idea es la misma: nos permite conocer la probabilidad de que nuestra variable aleatoria tome un cierto valor del espacio muestral.
Es importante mencionar que, aunque la probabilidad de que la variable aleatoria tome un valor específico es \(0\), ya que nos encontramos en un conjunto no numerable, sí que podemos calcular la probabilidad de que se encuentre entre dos valores. Por tanto, si la función de densidad es \(f_X\), entonces
\[ P\left[ a \le X \le b \right] = \int_{a}^{b}{f_X(x)dx} \]
La función de densidad tiene dos características importantes:
\[ \int_{-\infty}^{\infty}{f_X(x)\ dx} = 1 \]
Estas dos propiedades caracterizan a una función de densidad; es decir, toda función \(f: \mathbb{R} \rightarrow \mathbb{R}\) no negativa e integrable tal que \(\int_{-\infty}^{\infty}{f_X(x)\ dx} = 1\) es la función de densidad de alguna variable continua.
Intuitivamente, podemos ver esta última propiedad como si acumulamos todos los valores que puede tomar la variable aleatoria, la probabilidad de que te encuentres en el conjunto debe ser 1
Una de las variables aleatorias que más juego nos darán en el futuro será la v.a. con distribución uniforme en \([0, 1)\). La denotaremos \(\Xi \sim \mathcal{U}\left([0, 1)\right)\). La probabilidad de que \(\Xi\) tome un valor es constante, por lo que podemos definir su función de densidad como
\[ f_\Xi(\xi) = \left\{ \begin{array}{llc} 1 & \text{si } \xi \in [0, 1) \\ 0 & \text{en otro caso.} \end{array} \right. \]
La probabilidad de \(\Xi\) tome un valor entre dos elementos \(a, b \in [0, 1)\) es
\[ P(\Xi \in [a, b]) = \int_{a}^{b}{1dx} = b - a \]
Como veremos más adelante, definiendo correctamente una función de densidad conseguiremos mejorar el rendimiento del path tracer.
La función de distribución \(F_X(x)\) podemos definirla como:
\[ F_X(x) = P\left[ X \le x \right] = \int_{-\infty}^{x}{f_X(t)dt} \]
Es decir, dado un \(x\), ¿cuál sería la probabilidad de que \(X\) se quede por debajo de \(x\)?
Al igual que ocurre en el caso discreto, \(F_X\) toma valores entre 0 y 1 (\(0 \le F_X(x) \le 1\)) y sus límites laterales coinciden con las cotas anteriores (\(\lim_{x \to -\infty}{F_X} = 0\), \(\lim_{x \to \infty}{F_X} = 1\)).
El Teorema Fundamental del Cálculo nos permite relacionar función de distribución y función de densidad directamente:
\[ f_X(x) = \frac{dF_X(x)}{dx} \]
La esperanza de una variable aleatoria, denotada \(E\left[ X \right]\), es una generalización de la media ponderada. Nos informa del valor esperado de dicha variable aleatoria.
En el caso de las variables discretas, se define como
\[ E\left[ X \right] = \sum_{i}{x_i p_i} \]
donde \(x_i\) son los posibles valores que puede tomar la v.a., y \(p_i\) la probabilidad asociada a cada uno de ellos; es decir, \(p_i = P[X = x_i]\)
Para una variable aleatoria continua real, la esperanza viene dada por
\[ E\left[ X \right] = \int_{-\infty}^{\infty}{x f_X(x) dx} \]
Pongamos un par de ejemplos del cálculo de la esperanza. En el ejemplo de las variables discretas, la esperanza venía dada por
\[ E\left[ X \right] = \sum_{i = 2}^{12}{i P[X = i]} = 2\frac{1}{36} + 3 \frac{2}{36} + \dots + 12 \frac{1}{36} = 7 \]
Para variables aleatorias uniformes en \((a, b)\) (es decir, \(X \sim \mathcal{U}(a, b)\)), la esperanza es
\[ E\left[ X \right] = \int_{a}^{b}{x \frac{1}{b - a}dx} = \frac{a + b}{2} \]
La esperanza tiene unas cuantas propiedades que nos resultarán muy útiles. Estas son:
Estas propiedades no necesitan que las variables aleatorias sean independientes, lo cual supondrá un punto clave para las técnicas de Monte Carlo.
Será habitual encontrarnos con el problema de que no conocemos la distribución de una variable aleatoria \(Y\). Sin embargo, si encontramos una transformación medible de una variable aleatoria \(X\) de forma que obtengamos \(Y\) (esto es, \(\exists g\) función medible tal que \(g(X) = Y\)), entonces podemos calcular la esperanza de \(Y\) fácilmente. Esta propiedad hará que las variables aleatorias con distribución uniforme adquieran muchísima importancia. Generar números aleatorios en \([0, 1)\) es muy fácil, así que obtendremos otras vv.aa a partir de \(\Xi\).
Otra medida muy útil de una variable aleatoria es la varianza. Nos permitirá medir cómo de dispersa es la distribución con respecto a su media. La denotaremos como \(Var[X]\), y se define como
\[ Var[X] = E\left[ (X - E\left[ X \right])^2 \right] \]
Si desarrollamos esta definición, podemos conseguir una expresión algo más agradable:
\[ \begin{aligned} Var[X] & = E\left[ (X - E\left[ X \right])^2 \right] = \\ & = E\left[ X^2 + E\left[ X \right]^2 - 2XE\left[ X \right] \right] = \\ & = E\left[ X^2 \right] + E\left[ X \right]^2 - 2E\left[ X \right]E\left[ X \right] = \\ & = E\left[ X^2\right] - E\left[X \right]^2 \end{aligned} \]
Hemos usado que \(E\left[ E\left[ X \right] \right] = E\left[ X \right]\) y la linealidad de la esperanza.
Enunciemos un par de propiedades que tiene, similares a la de la esperanza:
La varianza nos será útil a la hora de medir el error cometido por una estimación de Monte Carlo.
Además de las anteriores propiedades, existen una serie de teoremas esenciales que necesitaremos más adelante:
Ley del estadístico insconciente (Law of the unconscious statistician, o LOTUS): dada una variable aleatoria \(X\) y una función medible \(g\), la esperanza de \(g(X)\) se puede calcular como
\[ E\left[ g(X) \right] = \int_{-\infty}^{\infty}{g(x) f_X(x) dx} \](26)
Ley (fuerte) de los grandes números: dada una muestra de \(N\) valores \(X_1, \dots, X_N\) de una variable aleatoria \(X\) con esperanza \(E\left[ X \right] = \mu\),
\[ P\left[ \lim_{N \to \infty}{\frac{1}{N} \sum_{i = 1}^{N}{X_i}} = \mu \right] = 1 \]
Usando que \(\bar{X}_N = \frac{1}{N} \sum_{i = 1}^{N}{X_i}\), esta ley se suele escribir como
\[ P\left[ \lim_{N \to \infty}{\bar{X}_N} = \mu \right] = 1 \](27)
Este teorema es especialmente importante. En esencia, nos dice que cuando repetimos muchas veces un experimento, al promediar los resultados obtendremos una esperanza muy cercana a la esperanza real.
Teorema Central del Límite (CLT) para variables idénticamente distribuidas (Owen 2013, capítulo 2): Sean \(X_1, \dots, X_N\) muestras aleatorias simples de una variable aleatoria \(X\) con esperanza \(E\left[ X \right] = \mu\) y varianza \(Var[X] = \sigma^2\). Sea
\[ Z_N = \frac{\sum_{i = 1}^{N}{X_i - N\mu}}{\sigma \sqrt{N}} \]
Entonces, la variable aleatoria \(Z_N\) converge hacia una función de distribución normal estándar cuando \(N\) es suficientemente grande:
\[ \lim_{N \to \infty}{P[Z_N \le z]} = \int_{-\infty}^{z}{\frac{1}{\sqrt{2 \pi}} e^{- \frac{x^2}{2}}dx} \](28)
A veces, no podremos conocer de antemano el valor que toma un cierto parámetro de una distribución. Sin embargo, conocemos el tipo de distribución que nuestra variable aleatoria \(X\) sigue. Los estimadores nos proporcionarán una forma de calcular el posible valor de esos parámetros a partir de una muestra de \(X\).
Sea \(X\) una variablea aleatoria con distribución perteneciente a una familia de distribuciones paramétricas \(X \sim F \in \left\{F(\theta) \,\middle|\, \theta \in \Theta \right\}\). \(\Theta\) es el conjunto de valores que puede tomar el parámetro. Buscamos una forma de determinar el valor de \(\theta\).
Diremos que \(T(X_1, \dots, X_N)\) es un estimador de \(\theta\) si \(T\) toma valores en \(\Theta\).
A los estimadores de un parámetro los solemos denotar con \(\hat{\theta}\).
Como vemos, la definición no es muy restrictiva. Únicamente le estamos pidiendo a la función de la muestra que pueda tomar valores viables para la distribución.
Se dice que un estimador \(T(X_1, \dots, X_N)\) es insesgado (o centrado en el parámetro \(\theta\)) si
\[ E\left[ T(X_1, \dots, X_n) \right] = \theta\quad \forall \theta \in \Theta \]
Naturalmente, decimos que un estimador \(T(X_1, \dots, X_N)\) está sesgado si \(E\left[ T(X_1, \dots, X_N) \right] \not = \theta\).
Tras este breve repaso de probabilidad, estamos en condiciones de definir el estimador de Monte Carlo. Primero, vamos con su versión más sencilla.
Los estimadores de Monte Carlo nos permiten hallar la esperanza de una variable aleatoria, digamos, \(Y\), sin necesidad de calcular explícitamente su valor. Para ello, tomamos \(N\) muestras \(Y_1, \dots, Y_N\) de \(Y\), cuya media vale \(\mu\). Entonces, el estimador de \(\mu\) (Owen 2013, capítulo 2) es:
\[ \hat\mu_N = \frac{1}{N} \sum_{i = 1}^{N}{Y_i} \](29)
La intuición del estimador es, esencialmente, la misma que la del teorema central del límite. Lo que buscamos es una forma de calcular el valor promedio de un cierto suceso aleatorio, pero lo único que podemos usar son muestras de su variable aleatoria. Promediando esas muestras, sacamos información de la distribución. En este caso, la media.
En cualquier caso, la existencia de este estimador viene dada por la ley de los grandes números (tanto débil como fuerte [27]). Si \(\mu = E\left[ Y \right]\), se tiene que
\[ \lim_{N \to \infty}P\left[ \left\lvert \hat\mu_N - \mu \right\rvert \le \varepsilon \right] = 1 \quad \forall\ \varepsilon > 0 \]
o utilizando la ley de los números grandes,
\[ \lim_{N \to \infty}P\left[ \left\lvert \hat\mu_N - \mu \right\rvert = 0 \right] = 1 \]
Haciendo la esperanza de este estimador, vemos que
\[ \begin{aligned} E\left[ \hat\mu_N \right] & = E\left[ \frac{1}{N} \sum_{i = 1}^{N}{Y_i}\right] = \frac{1}{N} E\left[\sum_{i = 1}^{N}{Y_i} \right] \\ & = \frac{1}{N} \sum_{i = 1}^{N}{E\left[ Y_i \right]} = \frac{1}{N} \sum_{i = 1}^{N}{\mu} = \\ & = \mu \end{aligned} \]
Por lo que el estimador es insesgado. Además, se tiene que la varianza es
\[ E\left[ (\hat\mu_N - \mu)^2 \right] = \frac{\sigma^2}{N} \]
Un ejemplo clásico de estimador de Monte Carlo es calcular el valor de \(\pi\). Se puede hallar integrando una función que valga \(1\) en el interior de la circunferencia de radio unidad y \(0\) en el exterior:
\[ \begin{aligned} f = \begin{cases} 1 & \text{si } x^2 + y^2 \le 1 \\ 0 & \text{en otro caso} \end{cases} \Longrightarrow \pi = \int_{-1}^{1} \int_{-1}^{1}{f(x, y)}\ dxdy \end{aligned} \]
Para usar el estimador de [30], necesitamos saber la probabilidad de obtener un punto dentro de la circunferencia.
Bien, consideremos que una circunferencia de radio \(r\) se encuentra inscrita en un cuadrado. El área de la circunferencia es \(\pi r^2\), mientras que la del cuadrado es \((2r)^2 = 4r^2\). Por tanto, la probabilidad de obtener un punto dentro de la circunferencia es \(\frac{\pi r^2}{4r^2} = \frac{\pi}{4}\). Podemos tomar \(p(x, y) = \frac{1}{4}\), de forma que
\[ \pi \approx \frac{4}{N} \sum_{i = 1}^{N}{f(x_i, y_i)}, \text{ con } (x_i, y_i) \sim \mathcal{U}(\small{[-1, 1] \times [-1, 1]}) \]
Generalmente nos encontraremos en la situación en la que \(Y = f(X)\), donde \(X \in S \subset \mathbb{R}^d\) sigue una distribución con función de densidad \(p_X(x)\) con media \(\mu = E\left[ X \right]\), y \(f: S \rightarrow \mathbb{R}\).
Nota(ción): nos encontramos ante un caso de “choque de notaciones”. Tradicionalmente las funciones de densidad utilizan \(f\), pero en transporte de luz se suele reservar esta letra para las BRDF y/u otras funciones genéricas, dejando la letra \(p\) para las funciones de densidad.
En este capítulo usaré la notación \(p_X\) para dejar claro de que estamos hablando de una función de densidad, manteniendo \(f\) para la transformación de la variable aleatoria.
Consideremos el promedio de \(N\) muestras de \(f(X)\):
\[ \frac{1}{N} \sum_{i = 1}^{N}{f(X_i)} \]
siendo \(X_1 \dots X_N\) idénticamente distribuidas. En ese caso, la esperanza es
\[ \begin{aligned} E\left[ \frac{1}{N} \sum_{i = 1}^{N}{f(X_i)} \right] & = E\left[\frac{1}{N} \sum_{i = 1}^{N}{f(X)} \right] = \\ & = \frac{1}{N} N E\left[ f(X) \right] = \\ & = E\left[ f(X) \right] = \\ & = \int_S f(x) p_X(x) dx \end{aligned} \]
¡Genial! Esto nos da una forma de calcular la integral de una función usando las imágenes de \(N\) muestras \(f(X_1), \dots, f(X_N)\) de una variable aleatoria \(X \sim p_X\). A este estimador de Monte Carlo lo llamaremos \(\hat{I}_N\):
\[ \begin{aligned} \hat{I}_N & = \frac{1}{N} \sum_{i = 1}^{N}{f(X_i)} \\ \Rightarrow E\left[ \hat{I}_N \right] & = \int_S f(x) p_X(x) dx \end{aligned} \](30)
Nota(ción): si te preguntas por qué lo llamamos \(\hat{I}_N\), piensa que queremos calcular la intergal \(I = \int_{S}{f(x)p_X(x)dx}\). Para ello, usamos el estimador \(\hat{I}\), y marcamos explícitamente que usamos \(N\) muestras.
La varianza del estimador se puede calcular fácilmente utilizando las propiedades que vimos en la sección de la varianza:
\[ \begin{aligned} Var\left[ \hat{I}_N \right] & = Var\left[ \frac{1}{N} \sum_{i = 1}^{N}{f(X_i)} \right] = \\ & = \frac{1}{N^2} Var\left[ \sum_{i = 1}^{N}{f(X_i)} \right] = \\ & = \frac{1}{N^2} N Var\left[ f(X) \right] = \\ & = \frac{1}{N} Var\left[ f(X) \right] \end{aligned} \](31)
Como es natural, el número de muestras que usemos será clave para la proximidad de la estimación. ¿Cómo de lejos se queda del valor real de la integral \(E\left[ f(X) \right]\)? Es decir; ¿cómo modifica \(N\) la varianza del estimador \(Var\left[ \hat{I}_N \right]\)?
Para comprobarlo, debemos introducir dos nuevos teoremas: la desigualdad de Markov y la desigualdad de Chebyshsev (Illana 2013, Introducción).
Desigualdad de Markov: Sea \(X\) una variable aleatoria que toma valores no negativos, y sea \(p_X\) su función de densidad. Entonces, \(\forall x > 0\),
\[ \begin{aligned} E\left[ X \right] & = \int_0^x t p_X(t)\ dt + \int_x^\infty t p_X(t)\ dt \ge \int_x^\infty t p_X(t)\ dt \\ & \ge \int_x^\infty x p_X(t)\ dt = x P\left[ X \ge x \right] \\ & \Rightarrow P\left[ X \ge x \right] \le \frac{E\left[ X \right]}{x} \end{aligned} \](32)
Desigualdad de Chebyshev: Sea \(X\) una variable aleatoria con esperanza \(\mu = E\left[ X \right]\) y varianza \(\sigma^2 = E\left[ (X - \mu)^2 \right]\). Entonces, aplicando la desigualdad de Markov [32] a \(D^2 = (X - \mu)^2\) se tiene que
\[ \begin{aligned} P\left[ D^2 \ge x^2 \right] & \le \frac{\sigma^2}{x^2} \\ \iff P\left[ \left\lvert X - \mu \right\rvert \ge x \right] & \le \frac{\sigma^2}{x^2} \end{aligned} \](33)
Ahora que tenemos estas dos desigualdades, apliquemos la de Chebyshev a [30] con \(\sigma^2 = Var\left[ \hat{I}_N \right]\), \(x^2 = \sigma^2/\varepsilon, \varepsilon > 0\):
\[ P\left[ \left\lvert \hat{I}_N - E\left[ \hat{I}_N \right] \right\rvert \ge \left(\frac{Var[\hat{I}_N]}{\varepsilon}\right)^{1/2} \right] \le \varepsilon \]
Esto nos dice que, usando un número de muestras relativamente grande (\(N >> \frac{1}{\varepsilon}\)), es prácticamente imposible que el estimador se aleje de \(E\left[ f(X) \right]\).
La desviación estándar puede calcularse fácilmente a partir de la varianza:
\[ \sqrt{Var[\hat{I}_N]} = \frac{\sqrt{Var\left[ f(X) \right]}}{\sqrt{N}} \](34)
así que, como adelantamos al inicio del capítulo, la estimación tiene un error del orden \(\mathcal{O}(N^{-1/2})\). Esto nos dice que, para reducir el error a la mitad, debemos tomar 4 veces más muestras.
Es importante destacar la ausencia del parámetro de la dimensión. Sabemos que \(X \in S \subset \mathbb{R}^d\), pero en ningún momento aparece \(d\) en la expresión de la desviación estándar [34]. Este hecho es una de las ventajas de la integración de Monte Carlo.
Hagamos un ejemplo práctico para visualizar lo que hemos aprendido en el software estadístico R.
Supongamos que queremos integrar la función \(f: [0, 1] \rightarrow \mathbb{R}\), \(f(x) = 2x^4\). Es decir, queremos calcular
\[ \int_0^1{2x^4\ dx} \]
El valor de esta integral es \(2 \left[\frac{x^5}{5}\right]_0^1 = 2/5 = 0.4\).
Primero, definimos la función \(f\):
f <- function(x) {
2 * x^4 * (x > 0 & x < 1)
}Tomamos N muestras en el intervalo \([0, 1]\) de forma uniforme:
N <- 1000
x <- runif(N) # x1, ...., xn
f_x <- sapply(x, f) # f(x1), ..., f(xn)
mean(f_x) # -> 0.3891845Observamos que el valor se queda muy cerca de \(0.4\). El error en este caso es \(0.4 - 0.3891845 = 0.01081546\).
Es interesante estudiar cómo de rápido converge el estimador al valor de la integral. Con el siguiente código, podemos caclular el error en función del número de muestras \(N\):
# Calcular la media y su error
estimacion <- cumsum(f_x) / (1:N)
error <- sqrt(cumsum((f_x - estimacion)^2)) / (1:N)
# Gráfico
plot(1:N, estimacion,
type = "l",
ylab = "Aproximación y límites del error (1 - alpha = 0.975)",
xlab = "Número de simulaciones",
)
z <- qnorm(0.025, lower.tail = FALSE)
lines(estimacion - z * error, col = "blue", lwd = 2, lty = 3)
lines(estimacion + z * error, col = "blue", lwd = 2, lty = 3)
abline(h = 0.4, col = 2)Este código produce la siguiente gráfica:
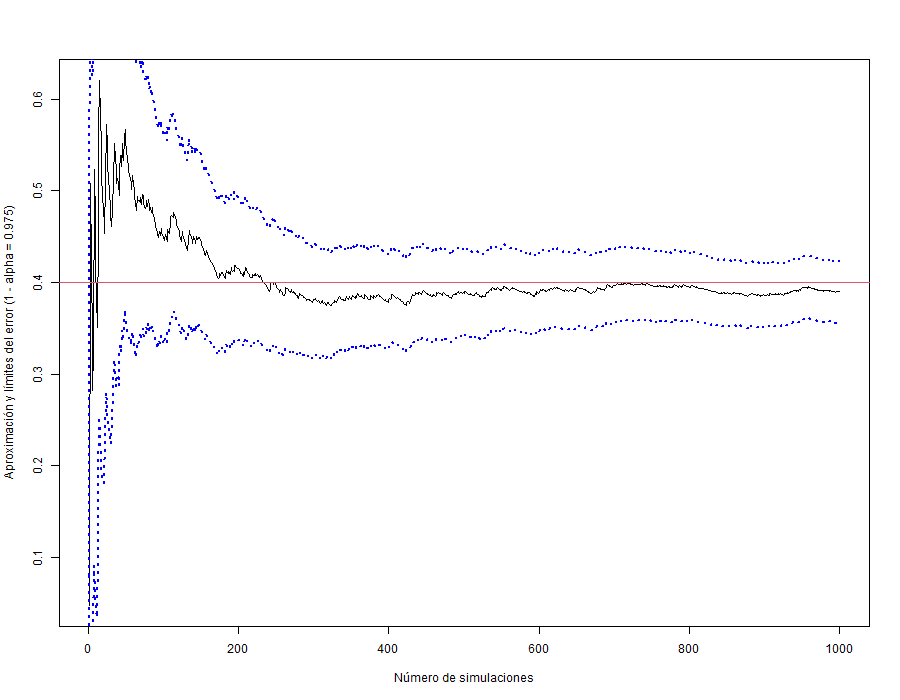
Se puede ver cómo debemos usar un número considerable de muestras, alrededor de 200, para que el error se mantenga bajo control. Aún así, aumentar el tamaño de \(N\) no disminuye necesariamente el error; nos encontramos en una situación de rendimientos decrecientes.
Como hemos visto, \(Var\left[ \hat{I}_N \right]\) depende del número de muestras \(N\) y de \(Var\left[ f(X) \right]\). Aumentar el tamaño de \(N\) es una forma fácil de reducir la varianza, pero rápidamente llegaríamos a una situación de retornos reducidos (Pharr, Jakob, and Humphreys 2016, The Monte Carlo Estimator). ¿Podemos hacer algo con el término \(Var\left[ f(X) \right]\)?
Vamos a jugar con él.
La integral que estamos evaluando ahora mismo es \(\int_S{f(x)p_X(x)}dx\), con \(p_X\) una función de densidad sobre \(S \subset \mathbb{R}^d\) \(\Rightarrow p_X(x) = 0\ \forall x \notin S\). Ahora bien, si \(q_X\) es otra función de densidad en \(\mathbb{R}^d\), entonces (Owen 2013, Importance Sampling):
\[ I = \int_S{f(x)p_X(x)dx} = \int_S{\frac{f(x)p_X(x)}{q_X(x)}q_X(x)dx} = E\left[ \frac{f(X)p_X(X)}{q_X(X)} \right] \]
Esta última esperanza depende de \(q_X\). Nuestro objetivo era encontrar \(E\left[ f(X) \right]\), pero podemos hacerlo tomando un término nuevo para muestrear desde \(q_X\) en vez de \(p_X\). Al factor \(\frac{p_X}{q_X}\) lo llamamos cociente de probabilidad, con \(q_X\) la distribución de importancia y \(p_X\) la distribución nominal.
No es necesario que \(q_X\) sea positiva en todo punto. Con que se cumpla que \(q_X(x) > 0\) cuando \(f(x)p_X(x) \not = 0\) es suficiente. Es decir, para \(Q = \left\{x \,\middle|\, q_X(x) > 0 \right\}\), tenemos que \(x \in Q\) cuando \(f(x)p_X(x) \not = 0\). Así, si \(x \in S \cap Q^c \Rightarrow f(X) = 0\), mientras que si \(x \in S^c \cap Q \Rightarrow p_X(X) \neq 0\). Entonces,
\[ \begin{aligned} E\left[ \frac{f(X)p_X(X)}{q_X(X)} \right] & = \int_Q{\frac{f(x)p_X(x)}{q_X(x)}q_X(x)dx} = \int_Q{f(x)p_X(x)dx} = \\ & = \int_Q{f(x)p_X(x)dx} + \int_{S^c \cap Q}{f(x)p_X(x)dx} - \int_{S \cap Q^c}{f(x)p_X(x)dx} = \\ & = \int_S{f(x)p_X(x)dx} = \\ & = E\left[ f(X) \right] \end{aligned} \]
De esta forma, hemos llegado al estimador de Monte Carlo por importancia:
\[ \tilde{I}_N = \frac{1}{N} \sum_{i=1}^N{\frac{f(X_i)p_X(X_i)}{q_X(X_i)}}, \quad X_i \sim q_X \](35)
Nota(ción): ¡fíjate en el gusanito! \(\hat{I}_N\) [30] y \(\tilde{I}_N\) tienen la misma esperanza, pero son estimadores diferentes.
Vamos a calcular ahora la varianza de este estimador. Sea \(\mu = E\left[ f(X) \right]\)
\[ \begin{aligned} Var\left[ \tilde{I}_N \right] & = \frac{1}{N} \left( \int_Q{\left(\frac{f(x)p_X(x)}{q_X(x)}\right)^2q_X(x) dx} - \mu^2 \right) = \\ & = \frac{1}{N} \textcolor{verde-oscurisimo}{\left( \int_Q{\frac{\left(f(x)p_X(x)\right)^2}{q_X(x)} dx} - \mu^2 \right)} = \\ & = \frac{\textcolor{verde-oscurisimo}{\sigma^2_q}}{N} \end{aligned} \]
La clave de este método reside en escoger una buena distribución de importancia. Puede probarse que la función de densidad que minimiza \(\sigma^2_q\) es proporcional a \(\left\lvert f(x) \right\rvert p_X(x)\) (Owen 2013, 6).
Esta técnica es especialmente importante en nuestra área de estudio. En transporte de luz, buscamos calcular el valor de la rendering equation [23]. Específicamente, de la integral
\[ \int_{H^2(\mathbf{n})}{BSDF(p, \omega_o \leftarrow \omega_i) L_i(p, \omega_i) \cos\theta_i\ d\omega_i} \]
que se suele representar como una simple integral sobre un cierto conjunto \(\int_S{f(x)dx}\). En la literatura se usa una versión modificada de muestreo por importancia:
\[ \tilde{I}_N = \frac{1}{N} \sum_{i=1}^N{\frac{f(X_i)}{p_X(X_i)}} \](36)
para que, utilizando muestras \(X_i \sim p_X\), \(E\left[ \frac{f}{p_X} \right] = \int_S{\frac{f}{p_X}p_X}\) y así se evalúe directamente la integral de \(f\). En cualquiera de los casos, el fundamento teórico es el mismo (Anderson 1999).
Esta forma de escribir el estimador nos permite amenizar algunos casos particulares. Por ejemplo, si usamos muestras \(X_i\) que sigan una distribución uniforme en \([a, b]\), entonces, su función de densidad es \(p_X(x) = \frac{1}{b - a}\). Esto da lugar a
\[ \tilde{I}_N = \frac{b - a}{N} \sum_{i = 1}^{N}{f(X_i)} \]
En lo que resta de capítulo, se utilizará indistintamente \(\frac{1}{N} \sum_{i=1}^N{\frac{f(X_i)p_X(X_i)}{q_X(X_i)}}\) o \(\frac{1}{N} \sum_{i=1}^N{\frac{f(X_i)}{p_X(X_i)}}\) según convenga. ¡Tenlo en cuenta!
Usando esta expresión, la distribución de importancia \(p_X\) que hace decrecer la varianza es aquella proporcional a \(f\). Es decir, supongamos que \(f \propto p_X\). Esto es, existe un \(s\) tal que \(f(x) = s p_X(x)\). Como \(p_X\) debe integrar uno, podemos calcular el valor de \(s\):
\[ \begin{aligned} \int_{S}{p_X(x)dx} & = \int_{S}{sf(x)dx} = 1 \quad \iff \\ s & = \frac{1}{\int_{S}{f(x)dx}} \end{aligned} \]
Y entonces, se tendría que
\[ \begin{aligned} Var\left[ \frac{f(X)}{p_X(X)}\right] & = Var\left[\frac{f(X)}{sf(X)} \right] = \\ & = Var\left[ \frac{1}{s} \right] = \\ & = 0 \end{aligned} \]
En la práctica, esto es inviable. El problema que queremos resolver es calcular la integral de \(f\). Y para sacar \(s\), necesitaríamos el valor de la integral de \(f\). ¡Estamos dando vueltas!
Por fortuna, hay algoritmos que son capaces de proporcionar la constante \(s\) sin necesidad de calcular la integral. Uno de los más conocidos es Metropolis-Hastings, del cual hablaremos posteriormente.
En este trabajo nos centraremos en buscar funciones de densidad \(p_X\) que se aproximen a \(f\) lo más fielmente posible, dentro del contexto del transporte de luz.
Pongamos un ejemplo de estimador de Monte Carlo para una caja de dimensiones \(\small{[x_0, x_1] \times [y_0, y_1] \times [z_0, z_1]}\). Si queremos estimar la integral de la función \(f: \mathbb{R}^3 \rightarrow \mathbb{R}\)
\[ \int_{x_0}^{x_1} \int_{y_0}^{y_1} \int_{z_0}^{z_1}{f(x, y, z)dx dy dz} \]
mediante una variable aleatoria \(X \sim \mathcal{U}(\small{[x_0, x_1] \times [y_0, y_1] \times [z_0, z_1]})\) con función de densidad \(p(x, y, z) = \frac{1}{x_1 - x_0} \frac{1}{y_1 - y_0} \frac{1}{z_1 - z_0}\), tomamos el estimador
\[ \tilde{I}_N = \frac{1}{(x_1 - x_0) \cdot (y_1 - y_0) \cdot (z_1 - z_0)} \sum_{i = 1}^{N}{f(X_i)} \]
Las técnicas de muestreo por importancia nos proporcionan estimadores para una integral de la forma \(\int{f(x)dx}\). Sin embargo, es frecuente encontrarse un producto de dos funciones, \(\int{f(x)g(x)dx}\). Si tuviéramos una forma de coger muestras para \(f\), y otra para \(g\), ¿cuál deberíamos usar?
Se puede utilizar un nuevo estimador de Monte Carlo, que viene dado por (Pharr, Jakob, and Humphreys 2016)
\[ \frac{1}{N_f} \sum_{i = 1}^{N_f}{\frac{f(X_i)g(X_i)w_f(X_i)}{p_f(X_i)}} + \frac{1}{N_g} \sum_{j = 1}^{N_g}{\frac{f(Y_j)g(Y_j)w_g(Y_j)}{p_g(Y_j)}} \]
donde \(N_f\) y \(N_g\) son el número de muestras tomadas para \(f\) y \(g\) respectivamente, \(p_f, p_g\) las funciones de densidad respectivas y \(w_f, w_g\) funciones de peso escogidas tales que la esperanza del estimador sea \(\int{f(x)g(x)dx}\).
Estas funciones peso suelen tener en cuenta todas las formas diferentes que hay de generar muestras para \(X_i\) e \(Y_j\). Por ejemplo, una de las que podemos usar es la heurística de balanceo:
\[ w_s(x) = \frac{N_s p_s(x)}{\sum_{i}{N_i p_i(x)}} \]
Una modificación de esta es la heurística potencial (power heuristic):
\[ w_s(x, \beta) = \frac{\left(N_s p_s(x)\right)^\beta}{\sum_{i}{\left(N_i p_i(x)\right)^\beta}} \]
la cual reduce la varianza con respecto a la heurística de balanceo. Un valor para \(\beta\) habitual es \(\beta = 2\).
Si queremos evaluar la contribución de luz en un punto teniendo en cuenta la luz directa, la expresión utilizada es
\[ L_o(p, \omega_o) = \int_{S^2}{f(p, \omega_o \leftarrow \omega_i) L_{directa}(p, \omega_i) \cos\theta_i\ d\omega_i} \]
Si utilizáramos muestreo por importancia basándonos en las distribuciones de \(L_{directa}\) o \(f\) por separado, algunas de las dos no rendiría especialmente bien. Combinando ambas mediante muestreo por importancia múltiple se conseguiría un mejor resultado.

Hasta ahora, la principal técnica estudiada ha sido muestreo por importancia (sea o no múltiple). Esto no quiere decir que sea la única. Al contrario; esas dos son de las más sencillas que se pueden usar.
En esta sección vamos a ver de forma breve otras formas de reducir la varianza de un estimador, centrádonos específicamente en el contexto de transporte de luz.
Un problema habitual en la práctica es saber cuándo terminar la propagación de un rayo. Una solución simple es utilizar un parámetro de profundidad –lo cual hemos implementado en el motor–. Otra opción más eficiente es utilizar el método de ruleta rusa.
En esencia, la idea es que se genere un número aleatorio \(\xi \in [0, 1)\). Si \(\xi < p_i\), el camino del rayo se continúa, pero multiplicando la radiancia acumulada por \(L_i(p, \omega_o \leftarrow \omega_i)/p_i\). En otro caso (i.e., si \(\xi \ge p_i\)), el rayo se descarta. Esto hace que se acepten caminos más fuertes, rechazando aquellas rutas con excesivo ruido.
Más información puede encontrarse en (Pharr, Jakob, and Humphreys 2016, Russian Roulette and Splitting).
Esta técnica recibe dos nombres. Tradicionalmente, se la conocía como muestreo directo de fuentes de luz, pero en los últimos años ha adoptado el nombre de next event estimation. Esencialmente, se trata de utilizar las luces de la escena para calcular la radiancia de un punto.
Podemos dividir la rendering equation [23] en dos sumandos (Ureña 2021):
\[ L(p, \omega_o) = L_e(p, \omega_o) + \underbrace{L_{directa}(p, \omega_o) + L_{indirecta}(p, \omega_o)}_{\text{La parte integral de la rendering equation}} \](37)
siendo \(L_e\) la radiancia emitida por la superficie, \(L_{directa}\) la radiancia reflejada debida únicamente a la incidente proveniente de las fuentes de iluminación y \(L_{indirecta}\) la radiancia indirecta.
\[ \begin{aligned} L_{directa} & = \int_{S^2}{f(p, \omega_o \leftarrow \omega_i) L_{e}(y, -\omega_i) \cos\theta_i\ d\omega_i} \\ L_{indirecta} & = \int_{S^2}{f(p, \omega_o \leftarrow \omega_i) L_{r}(y, \omega_o \leftarrow \omega_i) \cos\theta_i\ d\omega_i} \end{aligned} \](38)
siendo \(y\) el primer punto visible desde \(p\) en la dirección \(\omega_i\) situado en una fuente de luz.
En cada punto de intersección \(p\), escogeremos aleatoriamente un punto \(y\) en la fuente de luz, y calcularemos \(L_{directa}\). Esta integral es fácil de conseguir con las técnicas que ya conocemos. Sin embargo, \(L_{indirecta}\) cuesta más trabajo. Al aparecer la radiancia reflejada en el punto \(p, L_r(p, \omega_o \leftarrow \omega_i)\), necesitaremos evaluarla de forma recursiva trazando rayos en la escena.
Aunque estamos haciendo más cálculos en cada punto de la cadena de ray trace, al evaluar por separado \(L_{directa}\) y \(L_{indirecta}\) conseguimos reducir considerablemente la varianza. Por tanto, suponiendo fija la varianza, el coste computacional de un camino es mayor, pero el coste total es más bajo.
Esta técnica requiere conocer si desde el punto \(p\) se puede ver \(y\) en la fuente de luz. Es decir, ¿hay algún objeto en medio de \(p\) e \(y\)? Para ello, se suele utilizar lo que se conocen como shadow rays. Dispara uno de estos rayos para conocer si está ocluido.
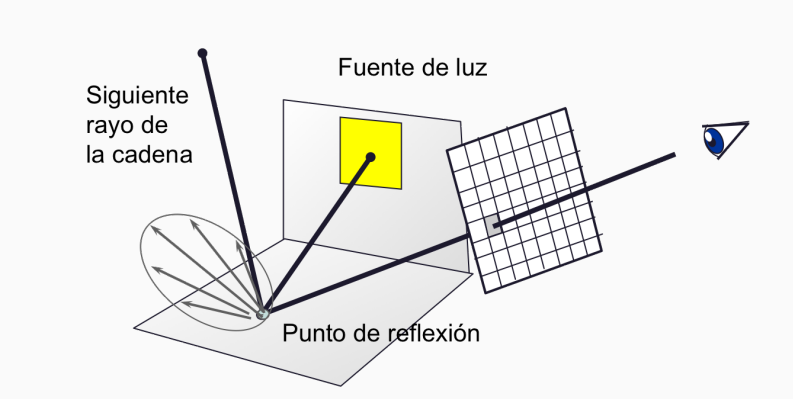
Si quieres informarte más sobre esta técnica, puedes leer (Moreau and Clarberg 2019).
Generalmente, en los estimadores de Monte Carlo se utilizan variables aleatorias distribuidas uniformemente a las que se le aplican transformaciones, pues resulta más sencillo generar un número aleatorio de la primera manera que de la segunda. La idea de los quasi-Monte Carlo es muestrear puntos que, de la manera posible, se extiendan uniformemente en \([0, 1]^d\); evitando así clústeres y zonas vacías (Owen 2013, Quasi-Monte Carlo).
Existen varias formas de conseguir esto. Algunas de las más famosas son las secuencias de Sobol, que son computacionalmente caras pero presentan menores discrepancias; o las series de Halton, que son más fáciles de conseguir.
Se puede estudiar el tema en profundidad en (Roberts 2018)

Una de las partes clave del estimador de Monte Carlo [30] es saber escoger la función de densidad \(p_X\) correctamente. En esta sección, veremos algunos métodos para conseguir distribuciones específicas partiendo de funciones de densidad sencillas, así como formas de elegir funciones de densidad próximas a \(f\). Los dos métodos principales que estudiaremos se han extraído del libro (Pharr, Jakob, and Humphreys 2016, Sampling Random Variables)
Este método nos permite conseguir muestras de cualquier distribución continua a partir de variables aleatorias uniformes, siempre que se conozca la inversa de la función de distribución.
Sea \(X\) una variable aleatoria con función de distribución \(F_X\)3. Queremos buscar una transformación \(T: [0, 1] \rightarrow \mathbb{R}\) tal que \(T(\xi) \stackrel{\text{\small d}}{=} X\), siendo \(\xi\) una v.a. uniformemente distribuida. Para que esto se cumpla, se debe dar
\[ \begin{aligned} F_X(x) & = P[X < x] = \\ & = P[T(\xi) < x] = \\ & = P(\xi < T^{-1}(x)) = \\ & = T^{-1}(x) \end{aligned} \]
Este último paso se debe a que, como \(\xi\) es uniforme en \((0, 1)\), \(P[\xi < x] = x\). Es decir, hemos obtenido que \(F_X\) es la inversa de \(T\).
En resumen: Para conseguir una muestra de una distribución específica \(F_X\), podemos seguir el siguiente algoritmo:
Como ejemplo, vamos a muestrear la función \(f(x) = x^2,\ x \in [0, 2]\) (“Computer graphics and imaging” 2022, Monte Carlo Integration).
Primero, normalizamos esta función para obtener una función de densidad \(p_X(x)\). Es decir, buscamos \(p_X(x) = c f(x)\) tal que
\[ \begin{aligned} 1 & = \int_{0}^{2}{p_X(x)dx} = \int_{0}^{2}{c f(x)dx} = c \int_{0}^{2}{f(x)dx} = \\ & = \left.\frac{cx^3}{3}\right\rvert_{2}^{3} = \frac{8c}{3} \\ & \Rightarrow c = \frac{3}{8} \\ & \Rightarrow p_X(x) = \frac{3x^2}{8} \end{aligned} \]
A continuación, integramos la función de densidad para obtener la de distribución \(F_X\):
\[ \begin{aligned} F_X(x) = \int_{0}^{x}{p_X(x)dx} = \int_{0}^{x}{\frac{3x^2}{8}} = \frac{x^3}{8} \end{aligned} \]
Solo nos queda conseguir la muestra. Para ello,
\[ \begin{aligned} \xi & = F_X(x) = \frac{x^3}{8} \quad \iff \\ x & = \sqrt[3]{8 \xi} \end{aligned} \]
Sacando un número aleatorio \(\xi\), y pasándolo por la función obtenida, conseguimos un elemento con distribución \(F(x)\).
Aunque el ejemplo anterior nos enseña cómo calcular a mano una función sencilla, resulta algo difícil de visualizar qué es lo que está ocurriendo. Por ello, vamos a utilizar el programa R para dar otro ejemplo.
Consideremos la distribución exponencial de parámetro \(\lambda\), la cual tiene función de densidad y de distribución
\[ \begin{aligned} f(x) & = \lambda e^{-\lambda x}, \quad & x \ge 0 \\ F(x) & = 1 - e^{-\lambda x}, \quad & x \ge 0 \end{aligned} \]
La función inversa se calcula tal que
\[ \begin{aligned} \xi & = F(x) = 1 - e^{-\lambda x} & \iff \\ x & = F^{-1}(\xi) = - \frac{log(1 - \xi)}{\lambda} & \end{aligned} \]
Generemos ahora \(\xi_1, \dots, \xi_n\) valores en \(\mathcal{U}(0, 1)\) y obtengamos las imágenes inversas \(X_i = -\frac{log(\xi_i)}{\lambda}\).
Para el ejemplo, fijemos \(\lambda = 1.5\) y calculemos los valores para \(X_i\):
F <- function(xi, lambda) {
-log(xi) / lambda
}
N <- 1000
xi <- runif(N)
lambda <- 1.5
x <- F(xi, lambda)Es fácil comprobar que los valores generados se asemejan fielmente a la función de densidad exponencial:
hist(x, freq = FALSE, breaks = 'FD', main = 'Método de la inversa para la exponencial', ylim = c(0, 1.5))
lines(density(x), col = 'blue')
curve(dexp(x, rate = lambda), add = TRUE, col = 2)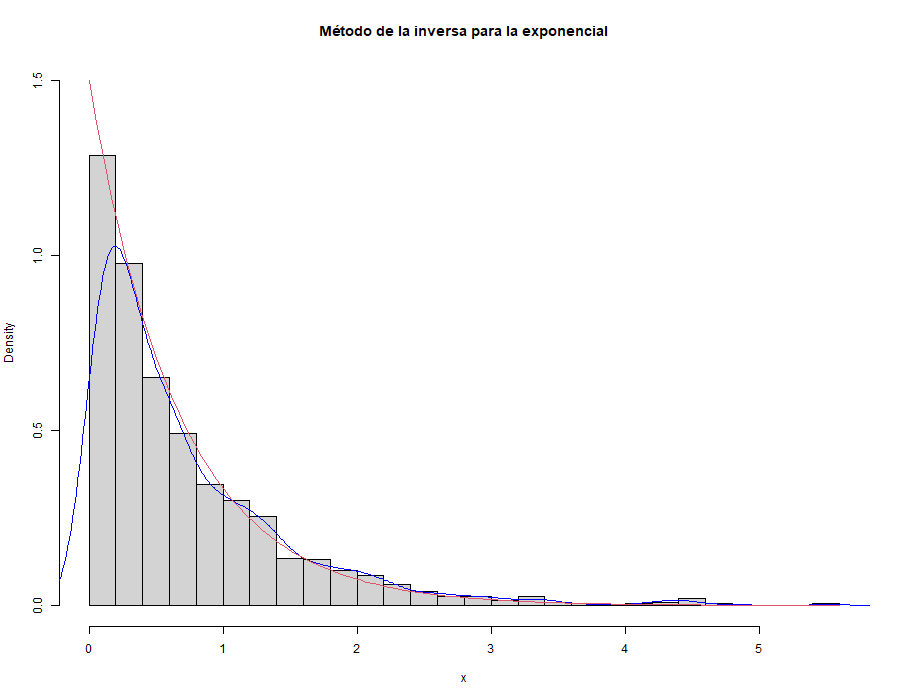
El método anterior presenta principalmente dos problemas:
Como alternativa, existe el método del rechazo o aceptación-rechazo (en inglés, rejection method) (Owen 2013, Non-uniform random variables). Necesitamos una variable aleatoria \(Y\) con función de densidad \(p_Y(y)\) de la cual resulta sencillo generar muestras. El objetivo es conseguir muestras de \(X \sim p_X\).
Como premisa, debemos buscar un \(M \in [1, \infty)\) tal que
\[ p_X(x) \le M p_Y(x) \quad \forall x \in \mathbb{R} \]
La idea principal es sacar una muestra de \(Y\) y aceptarla con probabilidad \(p_X/Mp_Y\). En otro caso, desecharla y volver a sacar otra. Para evitar casos absurdos, se puede especificar que \(p_Y(y)\) sea 0 cuando \(p_X(y)\) lo sea.
El valor más pequeño que podemos tomar para \(M\) es \(\sup_x{\frac{p_X(x)}{p_Y(x)}}\). De hecho, debemos buscar cotas próximas a este supremo, pues hará que el método sea más eficiente.
En esencia, estamos jugando a los dardos: si la muestra de \(y\) que hemos obtenido se queda por debajo de la gráfica de la función \(Mp_Y < p_X\), estaremos obteniendo una de \(p_X\).
El algoritmo consiste en:
Probemos por qué este algoritmo produce una muestra de la función de densidad \(p_X\):
Sea \(Y \sim p_Y\), \(\xi \sim \mathcal{U}(0, 1)\) independientes. Dado \(Y = y\), el candidato es aceptado si se cumple que \(\xi \le \frac{p_X(y)}{Mp_Y(y)}\). La probabilidad de que \(Y\) sea aceptado es:
\[ \int_{-\infty}^{\infty}{p_Y(y) \frac{p_X(y)}{Mp_Y(y)} dy} = \int_{-\infty}^{\infty}{\frac{p_X(y)}{M} dy} = \frac{1}{M} \]
Ahora bien, para cualquier \(x \in \mathbb{R}\)
\[ \begin{aligned} P\left[ X \le x \right] & = \int_{-\infty}^{x}{ \underbrace{p_Y(y) \frac{p_X(y)}{Mp_Y(y)} dy}_{\text{Si } y \text{ se acepta}} + \underbrace{\left(1 - \frac{1}{M}\right) P\left[ X \le x \right]}_{\text{Si } y \text{ se rechaza}} } = \\ & = \frac{1}{M} \int_{-\infty}^{x}{p_X(y) dy} + \left(1 - \frac{1}{M}\right) P\left[ X \le x \right] \\ & = \int_{-\infty}^{\infty}{p_X(y) dy} \end{aligned} \]
Lo que nos dice que \(X \sim p_X\) como queríamos comprobar.
De la misma forma que hicimos con el método de la inversa, implementaremos un ejemplo gráfico de esta técnica en el software R. En este caso, generaremos valores de una distribución Beta a partir de la uniforme. Es decir, podemos tomar
\[ \begin{aligned} p_X (x) & = \frac{\Gamma(a + b)}{\Gamma(a) \Gamma(b)} x^{a - 1} (1 - x)^{b - 1}, \quad 0 \le x \le 1; a = 2, b = 6 \\ p_Y (x) & = 1, \quad 0 \le x \le 1 \end{aligned} \]
Como \(M\) podemos tomar
\[ M = \sup_{x}\frac{p_Y(x)}{p_X(x)} = \sup_{x}{p_X(x)} \]
En la sección anterior dijimos que este algoritmo es “como jugar a los dardos”. Pues bien, la figura [24] muestra la diana. El siguiente fragmento de código de R calcula este valor:
a <- 2
b <- 6
resultado <- optimize(
f = function(x) { dbeta(x, shape1 = a, shape2 = b) },
maximum = TRUE,
interval = c(0, 1)
)
# $maximum
# [1] 0.1666692
#
# $objective
# [1] 2.813143
M <- resultado$objective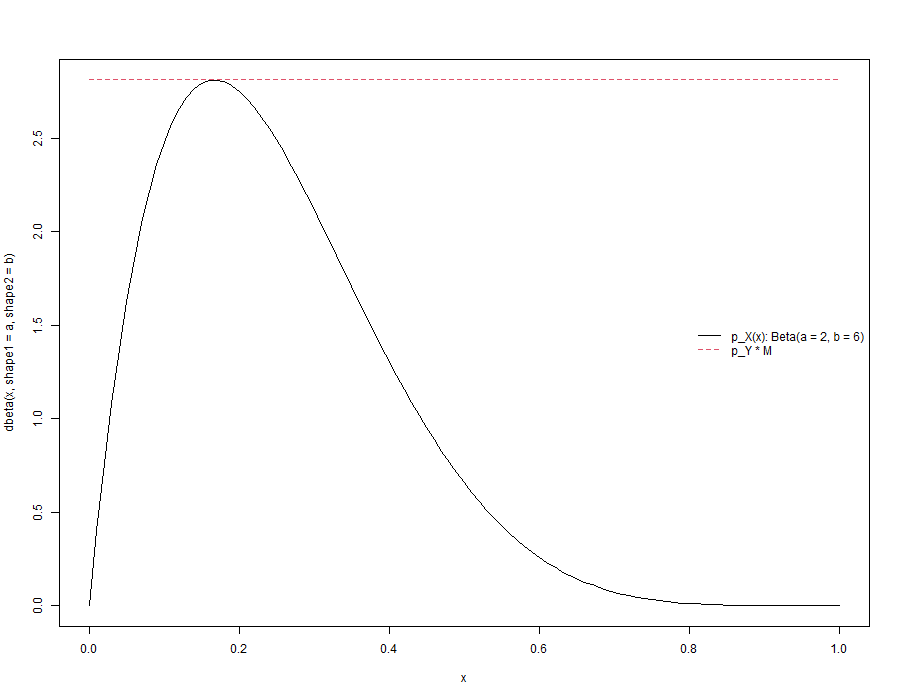
Para resolver el problema planteado, podemos usar el siguiente código:
N <- 1000
x <- double(N)
p_X <- function(x) dbeta(x, shape1 = a, shape2 = b)
p_Y <- function(x) 1
valores_generados <- 0
for (i in 1:N) {
xi <- runif(1)
y <- runif(1)
valores_generados <- valores_generados + 1
while (xi > p_X(y) / (M * p_Y(y))) {
# Seguir generando hasta que aceptemos uno
xi <- runif(1)
y <- runif(1)
valores_generados <- valores_generados + 1
}
# Aceptar el valor
x[i] <- y
}El hecho de que exista una posibilidad de que falle evidencia que el algoritmo no es muy eficiente. De hecho, podemos ver una medida de las veces que ha fallado:
valores_generados
# [1] 2906Es decir, para sacar 1000 muestras válidas ha hecho falta generar 2906; casi 3 veces más de las que queríamos.
Finalmente, veamos cómo de buena es la aproximación:
hist(x, freq = FALSE, breaks = 'FD', main = 'Método del rechazo para la distribución Beta(a = 2, b = 6)')
lines(density(x), col = 'blue')
curve(dbeta(x, shape1 = a, shape2 = b), add = TRUE, col = 2)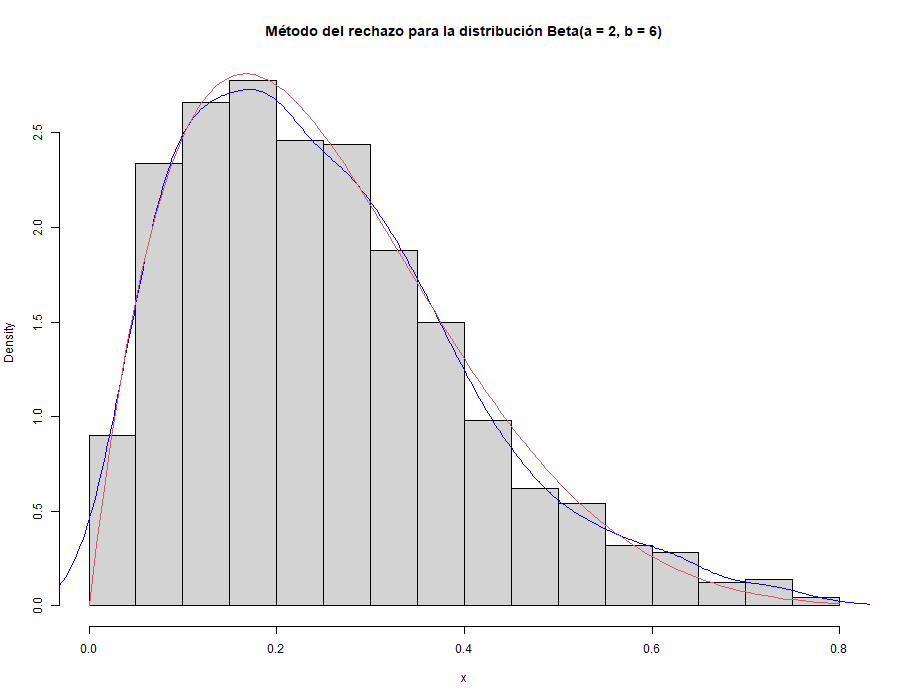
A lo largo de este capítulo hemos descrito las técnicas que se utilizan para aproximar los valores de una integral. En esta sección vamos a dar un salto de abstracción, e introduciremos brevemente cómo funcionan las cadenas de Markov, y cómo se pueden usar para aproximar soluciones de un tipo de ecuación integral denominada “ecuación de Fredholm de tipo 2”. Nos basaremos en los contenidos de (Farnoosh and Ebrahimi 2008) y (Tolver 2016).
Este tipo de ecuaciones resulta de interés puesto que la ecuación del transporte de luz es un caso particular de estas ecuaciones, pero con dominio infinito-dimensional.
Una ecuación de Fredholm de tipo 2 es una ecuación integral de la forma
\[ u(x) = f(x) + \lambda \int_{a}^{b}{k(x, t)u(t)\ dt} \](39)
Donde \(f(x) \in L_2\left([a, b]\right)\), \(k(x, t) \in L_2\left([a, b] \times [a, b]\right)\), el cual se denomina “kernel” de la ecuación de Fredholm; y \(u(x) \in L_2\left([a, b]\right)\), la cual es la función que queremos obtener.
El espacio \(L_2([a, b])\) se define como
\[ L_2([a, b]) = \left\{f \in L([a, b]) \,\middle|\, \int_{a}^{b}{\left\lvert f(t) \right\rvert^2\ dt} < \infty \right\} \]
Particularizaremos el caso \(a = 0, b = 1\), \(\lambda = 1\), \(0 \le x \le 1\) en lo que queda de sección.
Las cadenas de Markov son un tipo específico de proceso estocástico. Un proceso estocástico o aleatorio es una familia de variables aleatorias indexadas por otro conjunto. Si el conjunto es discreto, escribimos la familia como \(\left\{X(n)\right\}_{n \in \mathbb{N}}\), mientras que si es continuo, notaremos \(\left\{X(t)\right\}_{t \ge 0}\).
La distribución de los procesos estocásticos discretos en tiempo4 sobre un conjunto numerable \(S\) se viene caracterizado como
\[ P\left[ X(n) = i_n, \dots, X(0) = i_0 \right] \](40)
con \(i_n, \dots, i_0 \in S\), \(n \in \mathbb{N}\).
De la definición elemental de la probabilidad condicionada se sigue que
\[ \begin{aligned} & P\left[ X(n) = i_n, \dots, X(0) = i_0 \right] = \\ =\ & P\left[ X(n) = i_n \vert X(n - 1) = i_{n - 1}, \dots, X(0) = i_0 \right] \cdot \\ \cdot\ & P\left[ X(n - 1) = i_{n - 1} \vert X(n - 2) = i_{n-2}, \dots, X(0) = i_0 \right] \cdot \\ \cdot\ & \dots \\ \cdot\ & P\left[ X(1) = i_1 \vert X(0) = i_0 \right] \cdot \\ \cdot\ & P\left[ X(0) = i_0 \right] \end{aligned} \](41)
Una cadena de Markov en tiempo discreto (CMTD) sobre un conjunto numerable \(S\) es un proceso estocástico que satisface la propiedad de Markov; esto es,
\[ \begin{aligned} & P\left[ X(n) = i_n \vert X(n - 1) = i_{n - 1}, \dots, X(0) = i_0 \right] = \\ = & P\left[ X(n) = i_n \vert X(n - 1) = i_{n - 1} \right] \end{aligned} \](42)
para cualquier \(i_n, \dots, i_0 \in S\), \(n \in \mathbb{N}\). Esta propiedad nos dice que el estado en el paso \(n\) solo depende del estado inmediatamente anterior.
Resultará cómoda la siguiente notación
\[ P_{i, j}(n - 1) = P\left[ X(n) = j \vert X(n - 1) = i \right] \]
Se puede simplificar la expresión [41] utilizando la propiedad de Markov [42] y la anterior notación, de forma que obtenemos
\[ \begin{aligned} & P\left[ X(n) = i_n, \dots, X(0) = i_0 \right] = \\ = & P_{i_{n-1}, i_n}(n - 1) \cdot P_{i_{n-2}, i_{n-1}}(n - 2) \cdot \dots \cdot P_{i_0, i_{1}}(0) \cdot P\left[ X(0) = i_0 \right] \end{aligned} \]
A cada \(P_{i, j}(n)\) lo llamaremos probabilidad de transición en un paso en el instante \(n\), mientras que a \(P\left[ X(0) = i_0 \right]\) se le denominará la distribución inicial de probabilidades, denotado tal que
\[ \phi(i_0) = P\left[ X(0) = i_0 \right] \]
La distribución inicial de probabilidades proporciona la probabilidad de que la cadena se inicie en cualquier de los estados posibles.
Las cadenas de Markov discretas homogéneas en tiempo son aquellas para las que las probabilidades de transición no dependen de la indexación temporal \(n \in \mathbb{N}\); es decir, \(P_{i, j}(n) = P_{i, j} \quad \forall n \in \mathbb{N}\).
Por lo tanto, para este tipo de cadenas tenemos que
\[ \begin{aligned} P\left[ X(n) = i_n, \dots, X(0) = i_0 \right] = P_{i_{n-1}, i_n} \cdot \dots \cdot P_{i_0, i_{1}} \cdot \phi(i_0) \end{aligned} \](43)
De manera análoga, se pueden definir las cadenas de Markov en tiempo continuo homogéneas (CMTC homogéneas) sobre un conjunto numerable \(S\) como una familia de variables aleatorias \(\left\{X(t)\right\}_{t \ge 0}\) sobre un espacio de probabilidad \((\Omega, \mathbb{F}, P)\) de forma que
\[ \begin{aligned} & P\left[ X(s+t) = j \vert X(s) = i, X(u)\ 0 \le u \le s \right] = \\ = & P\left[ X(s+t) = j \vert X(s) = i \right] \end{aligned} \]
Con \(t,s \ge 0\). La distribución de la cadena viene determinada por la distribución inicial
\[ \phi(i) = P\left[ X(0) = i \right] \]
y la probabilidad de transición
\[ P_{i, j} = P\left[ X(t + s) = j \vert X(s) = i \right] \]
Las cadenas de Markov en tiempo continuo homogéneas cumplen la siguiente propiedad:
\[ \begin{aligned} P_{i, j}(s + t) & = \sum_{k = 1}^{N}{P_{i, k}(s)P_{k, j}(t)} = \\ & = \sum_{k = 1}^{N}{P_{i, k}(t)P_{k, j}(s)} \end{aligned} \]
donde \(1 \le i \le N\), \(t, s \ge 0\).
Un algoritmo basado en cadenas de Markov muy famoso es el muestreo de Metrópolis (Pharr, Jakob, and Humphreys 2016, Metropolis Light Transport). Una de sus grandes ventajas es que puede generar muestras que sigan la distribución de valores de una función \(f\). Para hacerlo, no necesita nada más que evaluar dicha función, sin necesidad de integrarla. Además, en cada iteración del algoritmo se consiguen muestras usables, a diferencia de otros método como aceptación-rechazo. Tal es su potencia que ha creado un área específica en la informática gráfica, denominado Metropolis light transport.
En el trabajo de (Farnoosh and Ebrahimi 2008) los autores muestran una forma de resolver las ecuaciones integrales [39] utilizando cadenas de Markov continuas en el espacio \([0, 1]\).
Consideremos la ecuación [39] en forma de funcional
\[ u(x) = f(x) + (Ku)(x) \]
o, directamente, omitiendo \(x\):
\[ u = f + Ku \]
siendo \(K\) el operador integral de la ecuación original:
\[ (Ku)(x) = \int_{0}^{1}{k(x, t)u(t)dt} \]
Tenemos que \((Ku)(x)\) será la primera iteración de \(u\) con respecto al kernel \(k\). La segunda iteración viene dada por
\[ K((Ku))(x) = (K^2u)(x) = \int_0^1 \int_0^1 {k(x, t)k(t, t_1)u(t_1) dtdt_1} \]
Así, de forma de recursiva, se obtiene que
\[ K(K^{n-1}u)(x) = (K^n u)(x) = \int_0^1 {k(x, t_{n-1})K^{n-1}u(t_{n-1}) dt_{n-1}} \](44)
Si asumimos que
\[ \left\lvert K \right\rvert = \sup_{[0, 1]}{\int_0^1{\left\lvert k(x, t) \right\rvert dt} < 1} \]
entonces, se puede resolver la ecuación de Fredholm [39] aplicando la fórmula recursiva
\[ u^{(n+1)} = Ku^{(n)} + f, \quad n = 1, 2, \dots \]
Si \(u^{(0)} = 0\), \(K^0 \equiv 0\), entonces, la ecuación anterior se transforma en
\[ u^{(n + 1)} = f+ Kf + \dots + K^nf = \sum_{m = 0}^{n}{K^mf} \](45)
Está claro que
\[ \lim_{n \to \infty} u^{(n)} = \lim_{n \to \infty} \sum_{m = 0}^{n}{K^mf} = u \]
Cada \(u^n\) puede calcularse utilizando una cadena de Markov para hallar su solución. Para ello, consideramos una cadena continua de Markov con probabilidad de transición \(P_{i, j}\) y distribución inicial \(\phi(i)\), satisfaciendo que
\[ \begin{aligned} \int_0^1{P_{i, j}\ dj} & = 1 \\ \int_0^1{\phi(i)\ di} & = 1 \\ \end{aligned} \](46)
Consideramos ahora una función de pesos \(W_m\) para la cadena de Markov, que viene dada por la recursión
\[ \begin{aligned} W_m & = W_{m-1} \frac{k(x_{m -1}, x_m)}{P_{x_{m-1}, x_m}}, \quad m = 1, 2, \dots \\ W_0 & = 1 \end{aligned} \](47)
Definamos ahora una variable aleatoria \(\Gamma_n(h)\), la cual está asociada al camino aleatorio \(x_0 \rightarrow x_1 \rightarrow \dots \rightarrow x_n\):
\[ \Gamma_n(h) = \frac{h(x_0)}{\phi(x_0)} = \sum_{m = 0}^{n}{W_mf(x_m)} \](48)
donde \(h(x)\) es una función real.
Consideremos ahora el producto escalar de dos funciones \(h(x), u(x)\), el cual se define como
\[ \langle h, u \rangle = \int_0^1{h(x)u(x) dx} \](49)
El problema ahora se convierte en encontrar el valor del producto \(\langle h, u \rangle\), siendo \(u(x)\) la función solución de la ecuación de Fredholm.
Teorema: el valor del producto escalar \(\langle h, u^{(n + 1)} \rangle\) puede ser estimado mediante la esperanza de la variable aleatoria \(\Gamma_n(h)\); es decir,
\[ E\left[ \Gamma_n(h) \right] = \langle h, u^{(n + 1)} \rangle \]
Veamos por qué ocurre esto. Cada camino aleatorio \(x_0 \rightarrow x_1 \rightarrow \dots \rightarrow x_n\) tiene una probabilidad de
\[ P\left[ X(0) = x_0, X(1) = x_1, \dots, X(n) = x_n \right] = \phi(x_0) P_{x_0, x_1} P_{x_1, x_2} \dots P_{x_{n-1}, x_n} \]
Como la variable aleatoria \(\Gamma_n(h)\) está definida a lo largo del camino anterior, se tiene que
\[ E\left[ \Gamma_n(h) \right] = \int_0^1 \int_0^1 \dotsc \int_0^1 {\Gamma_n(h) \phi(x_0) P_{x_0, x_1} P_{x_1, x_2} \dots P_{x_{n-1}, x_n} \,dx_0dx_1\dots dx_n} \]
Usando [47] y [48], se puede obtener que
\[ \begin{aligned} E\left[ \Gamma_n(h) \right] & = E\left[ \frac{h(x_0)}{\phi(x_0)} \sum_{m = 0}^{n}{W_mf(x_m)} \right] = \\ & = \int_0^1 \int_0^1 \dotsc \int_0^1 { h(x_0) \sum_{m = 0}^{n} \Upsilon \Psi f(x_m) \phi(x_m) \,dx_0dx_1\dots dx_n } \end{aligned} \]
siendo
\[ \begin{aligned} \Upsilon & = k(x_0, x_1) k(x_1, x_2) \dots k(x_{m-1}, x_m), \\ \Psi & = P_{x_{m}, x_{m+1}} \dots P_{x_{n-1}, x_n} \end{aligned} \]
Usando [46], la integral anterior puede reescribirse como
\[ E\left[ \Gamma_n(h) \right] = \sum_{m = 0}^{n} \int_0^1 \int_0^1 \dotsc \int_0^1 { h(x_0) \Upsilon f(x_m) \,dx_0dx_1\dots dx_n } \]
Y finalmente, si tenemos en cuenta la n-ésima iteración [44], así como [45] y la definición de producto escalar \(\langle h, u \rangle\), deducimos
\[ E\left[ \Gamma_n(h) \right] = \left \langle h(x), \sum_{m = 0}^n {(K^mf)(x)} \right \rangle = \langle h(x), u^{(n+1)}(x) \rangle \]
Lo cual concluye la prueba.
Este teorema nos dice que \(\Gamma_n(h)\) es un estimador insesgado del producto escalar \(\langle h(x), u^{(n+1)}(x) \rangle\).
Los autores proponen una forma basada en Monte Carlo basado en la simulación de una cadena de Markov continua para estimar el valor de \(\langle h(x), u^{(n+1)}(x) \rangle\), el cual presentaremos a continuación:
Consideremos una cadena de Markov continua con función de probabilidad de transición
\[ P_{x, y} = p(x) \delta(y - x) + (1 - p(x))g(y), \qquad x, y \in [0, 1] \]
siendo \(\delta(y - x)\) la delta de Dirac en \(x\), \(g(x)\) una función de densidad en \([0, 1]\), y \(p(x)\) una función tal que \(0 < p(x) < 1\) y \(\int_0^1\frac{g(x)}{1 - p(x)} dx \le \infty\).
Para estimar \(\langle h, u^{(n+1)}\), segumos el siguiente proceso:
\[ x_0^{(s)} \rightarrow x_1^{(s)} \rightarrow \dots \rightarrow x_n^{(s)}, \qquad s = 1(1)/N \]
de la cadena de Markov presentada anteriormente.
\[ \Gamma^{(s)}_n(h) = \frac{h(x_0)}{p(x_0)} \sum_{m = 0}^n W^{(s)}_m f(x_m) \]
donde
\[ \begin{aligned} W_m & = \frac{ k\left(x^{(s)}_0, x^{(s)}_1\right) k\left(x^{(s)}_1, x^{(s)}_2\right) \dots k\left(x^{(s)}_{n - 1}, x^{(s)}_n\right) }{ P_{x^{(s)}_0, x^{(s)}_1} P_{x^{(s)}_1, x^{(s)}_2} \dots P_{x^{(s)}_{n - 1}, x^{(s)}_n} }, \quad m = 1, 2, \dots \\ W^{(s)}_0 & = 1 \end{aligned} \]
\[ \frac{1}{N} \sum_{s = 1}^N \Gamma^{(s)}_n(h) \approx \langle h, u^{(n+1)} \rangle \]
El paso (1) puede ser realizado mediante el siguiente algoritmo:
Algoritmo 1
input: el número de trayectoria N, la longitud de la cadena n, la función p(x), la función de densidad de probabilidad g(x) en [0, 1]
output: la cadena de Markov x_0^{(s)} -> x_1^{(s)} -> ... -> x_n^{(s)}
for s = 1 to N do
// Generar una trayectoria
generar x_0^{(s)} mediante la función de densidad p(x)
for m = 1 to n-1 do
generar un número aleatorio u uniformemente distribuido en (0, 1)
if p(x_m^{(s)}) > u then
calcular x_{m+1}^{(s)} = x_m^{(s)}
else
generar x_{m+1}^{(s)} desde la función de densidad de prob. g
fi
end
endAhora que hemos introducido toda la teoría necesaria, es hora de ponernos manos a la obra. En este capítulo escogeremos una serie de herramientas y con ellas implementaremos un pequeño motor de path tracing en tiempo real.
La implementación estará basada en Vulkan, junto al pequeño framework de nvpro-samples, que puede encontrarse en el repositorio (NVIDIA 2022a). Nuestro trabajo recogerá varias de las características que se muestran en dicho repositorio. Además, mantendremos el mismo espíritu que la serie de (Shirley 2020a), Ray Tracing In One Weekend.
El resultado final puede verse en el siguiente vídeo (Millán 2022c)
Hemos llegado a una de las partes más importantes de este trabajo. Es el momento de poner en concordancia todo lo que hemos visto a lo largo de los capítulos anteriores. Vamos a aplicar las técnicas de Monte Carlo a las ecuaciones vistas en radiometría, teniendo en cuenta las propiedades de los diferentes materiales.
El código ilustrado en las siguientes secciones está basado en el de (NVIDIA 2022a), aunque se pueden encontrar numerosísimas modificaciones en la literatura del sector.
Lo que buscamos en esta sección es aproximar el valor de la radiancia en un cierto punto, que dependerá de cada píxel dela pantalla. ¿Recuerdas la ecuación de dispersión [17]?
\[ L_o(p, \omega_o \leftarrow \omega_i) = \int_{\mathbb{S}^2}{f(p, \omega_o \leftarrow \omega_i)L_i(p, \omega_i)\left\lvert \cos\theta_i \right\rvert\ d\omega_i} \]
Recordemos que \(L_o(p, \omega_o \leftarrow \omega_i)\) es la radiancia reflejada en un punto \(p\) hacia la dirección \(\omega_o\) desde \(\omega_i\), \(f(p, \omega_o \leftarrow \omega_i)\) es la función de distribución de dispersión bidireccional (i.e., cómo refleja la luz el punto) y \(\cos\theta_i\) el ángulo que forman el ángulo sólido de entrada \(\omega_i\) y la normal en el punto \(p\), \(\mathbf{n}\): \(\left\lvert \cos\theta_i \right\rvert = \left\lvert \omega_i \cdot \mathbf{n} \right\rvert\).
Añadamos el término de radiancia emitida \(L_e(p, \omega_o)\), la cantidad de randiancia emitida por el material del punto \(p\):
\[ L(p, \omega_o) = L_e(p, \omega_o) + \int_{\mathbb{S}^2}{f(p, \omega_o \leftarrow \omega_i)L_i(p, \omega_i)\cos\theta_i} d\omega_i \]
Este valor \(L(p, \omega_o)\) es la radiancia total saliente (es decir, emitida más reflejada) desde el punto \(p\) hacia la dirección \(\omega_o\).
Podemos aproximar el valor de la integral utilizando el estimador de Monte Carlo comúnmente considerado en la industria, [35]:
\[ \begin{aligned} L_o(p, \omega_o \leftarrow \omega_i) & = \int_{\mathbb{S}^2}{f(p, \omega_o \leftarrow \omega_i)L_i(p, \omega_i)\cos\theta_i} d\omega_i \\ & \approx \frac{1}{N} \sum_{j = 1}^{N}{\frac{f(p, \omega_o \leftarrow \omega_j) L_i(p, \omega_j) \cos\theta_j}{P\left[ \omega_j \right]}} \end{aligned} \](50)
Con \(N \in \mathbb{Z}^+\), y \(P\left[ \omega \right]\) la función de densidad de \(\omega\). Con \(N\) suficientemente grande, se conseguiría un valor de radiancia relativamente acertado. Sin embargo, en algunos casos, podemos simplificar más el sumando.
Fijémonos en el denominador. Lo que estamos haciendo es tomar una muestra de un vector en la esfera. Si trabajamos con una BRDF en vez de una BSDF, usaríamos un hemisferio en vez de la esfera.
En el caso de la componente difusa, sabemos que la BRDF es \(f_r(p, \omega_o \leftarrow \omega_i) = \frac{\rho}{\pi}\) aplicando reflectancia lambertiana, así que
\[ \frac{1}{N} \sum_{j = 1}^{N}{\frac{(\rho / \pi) L_i(p, \omega_j) \cos\theta_j}{P\left[ \omega_j \right]}} \]
En la sección muestreo por importancia, introducimos la idea de buscar una función proporcional a \(f\) para con el fin de reducir el error. Podemos usar \(P\left[ \omega \right] = \frac{\cos\theta}{\pi}\), de forma que
\[ \frac{1}{N} \sum_{j = 1}^{N}{\frac{(\rho / \pi) L_i(p, \omega_j) \cos\theta_j}{(\cos\theta_j / \pi)}} = \frac{1}{N} \sum_{j = 1}^{N}{L_i(p, \omega_j) \rho} \](51)
Lo cual nos proporciona una expresión muy agradable para los materiales difusos.
Por lo general, no será posible simplificar hasta tal punto la expresión. Para BRDFs distintas de la difusa, algunas veces no podremos encontrar una forma de hacer muestreo por importancia de forma tan simple, en la cual la función de densidad sea proporcional a la BRDF.
Con lo que conocemos hasta ahora, podemos empezar a programar los shaders. Una primera implementación inspirada en la rendering equation [50] sería similar a lo siguiente:
L(p, omega, profundidad) {
emision = L_e(p, omega, profundidad)
if (profundidad <= profundidad_maxima) {
u = direccion_aleatoria()
prob = pdf(p, u, omega) // probabilidad de escoger la dir. u
y = intersecar(p, u)
theta = dot(normal(p), u)
L = emision
+ L(y, -u, profundidad + 1) * f_r(p, u, omega) * cos(theta) / prob
}
return L
}El término emision corresponde a \(L_e(p, \omega_o)\). Siempre lo añadimos,
pues en caso de que el objeto no emita luz, la contribución de este
término sería 0.
La principal desventaja de esta implementación es que utiliza recursividad. Como bien es conocido, abusar de recursividad provoca que el tiempo de ejecución aumente significativamente.
Como es natural, el tiempo es una limitación enorme para cualquier programa en tiempo real. Mientras que en un offline renderer disponemos de un tiempo muy considerable por frame (desde varios segundos hasta horas), en un programa en tiempo real necesitamos que un frame salga en 33.3 milisegundos o menos. Este concepto se suele denominar frame budget: la cantidad de tiempo que disponemos para un frame.
Nota: cuando hablamos del tiempo disponible para un frame, solemos utilizar milisegundos (ms) o frames por segundo (FPS). Para que un programa en tiempo real vaya suficientemente fluido, necesitaremos que el motor corra a un mínimo de 30 FPS (que equivalen a 33.3 ms/frame). Hoy en día, debido al avance del área en campos como los videosjuegos, el estándar se está convirtiendo en 60 FPS (16.6 ms/frame). Aún más, en los videojuegos competitivos profesionales se han asentado los 240 FPS (4.1 ms/frame).
Las nociones de los capítulos anteriores no distinguen entre un motor en tiempo real y offline. Como es natural, necesitaremos introducir unos pocos conceptos más para llevarlo a tiempo real. Además, existen una serie de requisitos hardware que debemos cumplir para que un motor en tiempo real con ray tracing funcione.
El requisito más importante de todos es la gráfica. Para ser capaces de realizar cálculos de ray tracing en tiempo real en escenarios complejos, necesitaremos una arquitectura moderna con núcleos dedicados a este tipo de cáclulos 5. Aunque es posible implementar ray tracing en gráficas convencionales, el rendimiento no será lo suficientemente bueno como para adecuarse al nivel de fidelidad de los tiempos actuales.
A día 17 de abril de 2022, para correr ray tracing en tiempo real, se necesita alguna de las siguientes tarjetas gráficas:
| Arquitectura | Fabricante | Modelos de gráficas |
|---|---|---|
| Turing | Nvidia | RTX 2060, RTX 2060 Super, RTX 2070, RTX 2070 Super, RTX 2080, RTX 2080 Super, RTX 2080 Ti, RTX Titan |
| Ampere | Nvidia | RTX 3050, RTX 3060, RTX 3060 Ti, RTX 3070, RTX 3070 Ti, RTX 3080, RTX 3080 Ti, RTX 3090, RTX 3090 Ti |
| RDNA2 (Navi 2X, Big Navi) | AMD | RX 6400, RX 6500 XT, RX 6600, RX 6600 XT, RX 6700 XT, RX 6800, RX 6800 XT, RX 6900 XT |
| Arc Alchemist | Intel | No reveleado aún |
Se puede encontrar más información sobre las diferentes arquitecturas y gráficas en el siguiente artículo de AMD Radeon (AMD 2021), Nvidia “Nvidia ampere architecture” (2021), e (Intel 2022a). Solo se han incluido las gráficas de escritorio de consumidor.
Para este trabajo se ha utilizado una RTX 2070 Super. En el capítulo de análisis del rendimiento se hablará con mayor profundidad de este apartado.
Una vez hemos cumplido los requisitos de hardware, es hora de escoger los frameworks de trabajo.
Las API de gráficos están empezando a adaptarse a los requisitos del tiempo real, por lo que cambian frecuentemente. La mayoría adquirieron las directivas necesarias muy recientemente. Aun así, son lo suficientemente sólidas para que se pueda usar en aplicaciones empresariales de gran embergadura.
Esta es una lista de las API disponibles con capacidades de Ray Tracing disponibles para, al menos, la arquitectura Turing:
De momento, no hay mucho donde elegir.
OptiX es la API más vieja de todas. Su primera versión salió en 2009, mientras que la última estable es de 2021. Tradicionalmente se ha usado para offline renderers, y no tiene un especial interés para este trabajo estando las otras dos disponibles.
Tanto DXR como Vulkan son los candidatos más sólidos. DXR salió en 2018, con la llegada de Turing. Es un par de años más reciente que Vulkan KHR. Cualquiera de las dos cumpliría su cometido de forma exitosa. Sin embargo, para este trabajo, hemos escogido Vulkan por los siguientes motivos:
Ambas API se comportan de manera muy similar, y no existe una gran diferencia entre ellas; tanto en rendimiento como en complejidad de desarrollo. Actualmente el proyecto solo compila en Windows 10 o mayor, por lo que estos dos puntos no resultan especialmente relevantes para el trabajo.
Si se desea, se puede encontrar una comparación más a fondo de las API en el blog de (Galvan 2022a). Además, el manual de Vulkan con las extensiones de KHR se puede encontrar en (The Khronos Vulkan Working Group 2022).
Un proyecto de Vulkan necesita una cantidad de código inicial considerable. Para acelerar este trámite y partir de una base más sólida, se ha decidido usar un pequeño framework de trabajo de Nvidia llamado [nvpro-samples] (NVIDIA 2022b).
Esta serie de repositorios de Nvidia DesignWorks contienen proyectos de ray tracing de Nvidia con fines didácticos. Nosotros usaremos vk_raytracing_tutorial_KHR (NVIDIA 2022a), pues ejemplifica cómo añadir ray tracing en tiempo real a un proyecto de Vulkan. En particular, nosotros seguiremos las siguientes secciones, pero extendiendo el resultado final:
vk_raytrace.Estos frameworks contienen asimismo otras utilidades
menores. Destacan GLFW (gestión de ventanas en C++),
imgui (interfaz de usuario) y
tinyobjloader (carga de .obj y
.mtl).
Nuestro repositorio utiliza las herramientas citadas anteriormente para compilar su proyecto. El Makefile es una modificación del que se usa para ejecutar los ejemplos de Nvidia. Por defecto, ejecuta una aplicación muy simple que muestra un cubo mediante rasterización, la cual modificaremos hasta añadir ray tracing en tiempo real. Por tanto, la parte inicial del desarrollo consiste en adaptar Vulkan para usar la extensión de ray tracing, extrayendo la información de la gráfica y cargando correspondientemente el dispositivo.

La estructura final de las carpetas del repositorio con el código
fuente del proyecto (es decir, la carpeta application) es
la siguiente:
application/build contiene todo lo
relacionado con CMake y el ejecutable final.application/nvpro_core. Se descargan automáticamente seguir
las instrucciones de compilación.application/vulkan_ray_tracing/media/ se encuentran
todos los archivos .obj, .mtl y las
texturas.application/vulkan_ray_tracing/src
contiene el código fuente de la propia aplicación.
engine.h/cpp. Una de las desventajas
de seguir un framework “de juguete” es que el acoplamiento es
considerablemente alto. Más adelante comentaremos los motivos.globals.hpp.scene.hpp.main.cpp se gestiona tanto el punto de entrada de la
aplicación como la actualización de la interfaz gráfica.application/vulkan_ray_tracing/src/shaders
contiene todos los shaders; tanto de rasterización, como de ray tracing.
raytrace.*,
pathtrace.glsl (que contiene el grueso del path
tracer).frag_shader.frag, passthrough.vert,
post.frag, vert_shader.vert.sampling.glsl (donde se implementan
distribuciones aleatorias) o random.glsl (que contiene
generadores de números aleatorios).application/vulkan_ray_tracing/src/spv contiene los shaders
compilados a SPIR-V.El diagrama 27 permite visualizar los puntos anteriores, así como la estructura general del repositorio.

Teniendo en cuenta que utilizamos un framework que no está pensado para producción y la naturaleza de Vulkan, realizar un diagrama de clase es muy complicado. Sin embargo, podemos ilustrar las clases más importantes de la aplicación: la el motor [28] y la de escenas [29] . En las secciones posteriores detallaremos algunos de los miembros de estas.
Una figura que se asemeja a un diagrama de secuencia específico para el loop de ray tracing puede encontrarse en [31].

Las dependencias necesarias son:
VK_KHR_ray_tracing_pipeline.Ejecuta los siguientes comandos desde la terminal para compilar el proyecto:
git clone --recursive --shallow-submodules https://github.com/Asmilex/Raytracing.git
cd .\Raytracing\application\vulkan_ray_tracing\
mkdir build
cd build
cmake ..
cmake --build .Si todo funciona correctamente, debería generarse un binario en
./application/bin_x64/Debug llamado
asmiray.exe. Desde la carpeta en la que deberías
encontrarte tras seguir las instrucciones, puedes conseguir ejecutarlo
con
..\..\bin_x64\Debug\asmiray.exeEl principal coste de ray tracing es el cálculo de las intersecciones con objetos; hasta un 95% del tiempo de ejecución total (Scratchapixel 2019). Reducir el número de test de intersección es clave.
Las estructuras de aceleración son una forma de representar la geometría de la escena. Aunque existen diferentes tipos, en esencia, todos engloban a uno o varios objetos en una estructura con la que resulta más eficiente hacer test de intersección en términos del tiempo. Fueron introducidos por primera vez en (Kay and Kajiya 1986).
Uno de los tipos más comunes (y el que se usa en (Shirley 2020b)) es la Bounding Volume Hierarchy (BVH). Fue una técnica desarrollada por (Kay and Kajiya 1986). Este método encierra un objeto en una caja (denomina una bounding box), de forma que el test de intersección principal se hace con la caja y no con la geometría. Si un rayo impacta en la bounding box, entonces se pasa a testear la geometría.
Se puede repetir esta idea repetidamente, de forma que agrupemos varias bounding boxes. Así, creamos una jerarquía de objetos –como si nodos de un árbol se trataran–. A esta jerarquía es a la que llamamos BVH.
Es importante crear buenas divisiones de los objetos en la BVH. Cuanto más compacta sea una BVH, más eficiente será el test de intersección.
Una forma habitual de crear la BVH es mediante la división del espacio en una rejilla. Esta técnica se llama Axis-Aligned Bounding Box (AABB). Usualmente se usa el método del slab (también introducido por Kay y Kajilla). Se divide el espacio en una caja n-dimensional alineada con los ejes, de forma que podemos verla como \([x_0, x_1] \times\) \([y_0, y_1] \times\) \([z_0, z_1] \times \dots\) De esta forma, comprobar si un rayo impacta en una bounding box es tan sencillo como comprobar que está dentro del intervalo. Este es el método que se ha usado en Ray Tracing in One Weekend.
Vulkan gestiona las estructuras de aceleración diviéndolas en dos partes: Top-Level Acceleration Structure (TLAS) y Bottom-Level Acceleration Structure (BLAS).
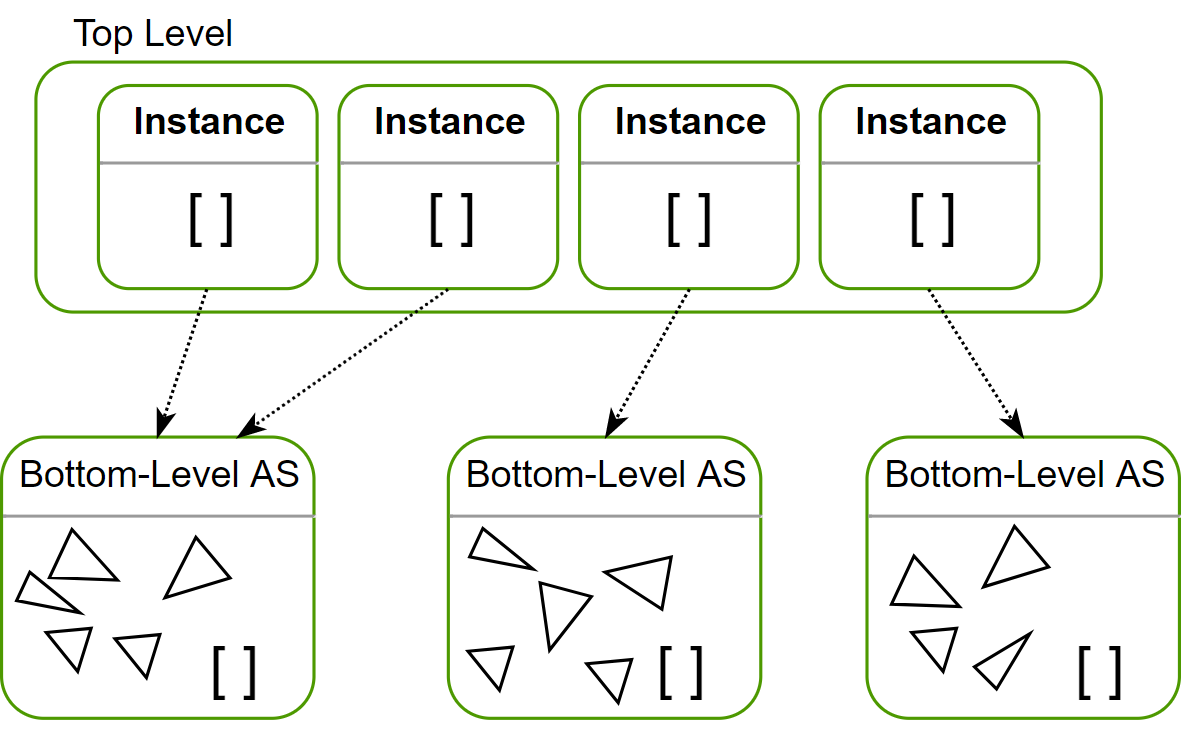
Las estructuras de aceleración de bajo nivel (Bottom-Level Acceleration Structure, BLAS) almacenan la geometría de un objeto individual; esto es, los datos de los vértices y los índices de los triángulos, además de una AABB que la encapsula.
Pueden almacenar varios modelos, puesto que alojan uno o más buffers de vértices junto a sus matrices de transformación. Si un modelo es instanciado varias veces dentro de la misma BLAS, la geometría se duplica. Esto se hace para mejorar el rendimiento.
Como regla general, cuantas menos BLAS, mejor (NVIDIA 2020b).
El código correspondiente a la creación de la BLAS en el programa es el siguiente:
void Engine::createBottomLevelAS() {
// BLAS - guardar cada primitiva en una geometría
std::vector<nvvk::RaytracingBuilderKHR::BlasInput> allBlas;
allBlas.reserve(m_objModel.size());
for (const auto& obj: m_objModel) {
auto blas = objectToVkGeometryKHR(obj);
// Podríamos añadir más geometrías en cada BLAS.
// De momento, solo una.
allBlas.emplace_back(blas);
}
m_rtBuilder.buildBlas(
allBlas,
VK_BUILD_ACCELERATION_STRUCTURE_PREFER_FAST_TRACE_BIT_KHR
);
}Las Top-Level Acceleration Structures almacenan las instancias de los objetos, cada una con su matriz de transformación y referencia a la BLAS correspondiente.
Además, guardan información sobre el shading. Así, los shaders pueden relacionar la geometría intersecada y el material de dicho objeto. En esta última parte jugará un papel fundamental la Shader Binding Table.
En el programa hacemos lo siguiente para construir la TLAS:
void Engine::createTopLevelAS() {
std::vector<VkAccelerationStructureInstanceKHR> tlas;
tlas.reserve(m_instances.size());
for (const HelloVulkan::ObjInstance& inst: m_instances) {
VkAccelerationStructureInstanceKHR rayInst{};
// Posición de la instancia
rayInst.transform = nvvk::toTransformMatrixKHR(inst.transform);
rayInst.instanceCustomIndex = inst.objIndex;
// returns the acceleration structure device address of the blasId. The id correspond to the created BLAS in buildBlas.
rayInst.accelerationStructureReference = m_rtBuilder.getBlasDeviceAddress(inst.objIndex);
rayInst.flags = VK_GEOMETRY_INSTANCE_TRIANGLE_FACING_CULL_DISABLE_BIT_KHR;
rayInst.mask = 0xFF; // Solo registramos hit si rayMask & instance.mask != 0
rayInst.instanceShaderBindingTableRecordOffset = 0; // Usaremos el mismo hit group para todos los objetos
tlas.emplace_back(rayInst);
}
m_rtBuilder.buildTlas(
tlas,
VK_BUILD_ACCELERATION_STRUCTURE_PREFER_FAST_TRACE_BIT_KHR
);
}Primero, debemos introducir unas nociones básicas de Vulkan sobre cómo gestiona la información que se pasa a los shaders.
Un resource descriptor (usualmente lo abreviaremos como descriptor) es una forma de cargar recursos como buffers o imágenes para que la tarjeta gráfica los pueda utilizar; concretamente, los shaders. El descriptor layout especifica el tipo de recurso que va a ser accedido, mientras que el descriptor set determina el buffer o imagen que se va a asociar al descriptor. Este set es el que se utiliza en los drawing commands. Un pipeline es una secuencia de operaciones que reciben una geometría y sus texturas, y la transforma en unos pixels.
Si necesitas más información, todos estos conceptos aparecen desarrollados extensamente en (Overvoorde 2022, Descriptor layout and buffer).
Tradicionalmente, en rasterización se utiliza un descriptor set por tipo de material, y consecuentemente, un pipeline por cada tipo. En ray tracing esto no es posible, puesto que no se sabe qué material se va a usar: un rayo puede impactar en cualquier material presente en la escena, lo cual invocaría un shader específico. Debido a esto, empaquetaremos todos los recursos en un único set de descriptores.
El pipeline de ray tracing soporta varios tipos de shaders diferentes que cubren la funcionalidad esencial de un ray tracer:
traceRayEXT(), la cual
se encarga de generar un nuevo rayo, solo ocurre desde este shader. La
implementación se encuentra en
application/vulkan_ray_tracing/src/shaders/raytrace.rgen.application/vulkan_ray_tracing/src/shaders/raytrace.rchit.application/vulkan_ray_tracing/src/shaders/raytrace_rahit.glsl.application/vulkan_ray_tracing/src/shaders/raytrace.rmiss.Existe otro tipo de shader adicional denominado callable shader. Este es un shader que se invoca desde otro shader, a modo de subrutina. Por ejemplo, un shader de intersección puede invocar a un shader de oclusión. Otro ejemplo sería un closest hit que reemplaza un bloque if-else por un shader para hacer cálculos de iluminación. Este tipo de shaders no se han implementado en el path tracer, pero se podrían añadir con un poco de trabajo.
En ray tracing, los shaders por sí solos no pueden realizar todos los cálculos necesarios para conseguir la imagen final. Necesitaremos enviar información externa a estos. Para conseguirlo tenemos diferentes mecanismos:
El primero de ellos son las push constants. Estas
son variables que se pueden traspasar a los shaders (es decir, de CPU a
GPU), pero que no se pueden modificar entre fases. Únicamente podemos
mandar un pequeño número de variables, el cual se puede consultar
mediante VkPhysicalDeviceLimits.maxPushConstantSize.
Además, es importante tener en cuenta el alineamiento de las estructuras
almacenadas.
Nuestro path tracer tiene implementado actualmente (19 de abril de 2022) las siguientes constantes:
struct PushConstantRay {
vec4 clearColor; // Color ambiental
vec3 lightPosition;
float lightIntensity;
int lightType;
int maxDepth; // Cuántos rebotes máximos permitimos
int nb_samples; // Para antialiasing
int frame; // Para acumulación temporal
};¿Y si queremos pasar información mutable entre shaders?
Para eso están los payloads. Cada rayo puede llevar
información adicional, que se conoce como carga. En esencia, es como una
pequeña mochila: el rayo puede recoger información de un shader y
pasarlo a otro. Esto resulta muy útil, por ejemplo, a la hora
de calcular la radiancia de un camino, o saber desde qué punto venía el
rayo. Se crean mediante la estructura rayPayloadEXT, y se
reciben en otro shader mediante rayPayloadInEXT. Es
importante controlar que el tamaño de la carga no sea excesivamente
grande.
Los payloads se definen de la siguiente manera:
struct HitPayload
{
vec3 hit_value;
vec3 weight;
vec3 ray_origin;
vec3 ray_dir;
int depth;
uint seed;
};Para solventar el problema de determinar el material de un objeto en ray tracing vamos usar la Shader Binding Table (SBT). Esta estructura permitirá cargar el shader correspondiente dependiendo de dónde impacte un rayo.
Para cargar esta estructura, se debe hacer lo siguiente:
VkShaderModule.VkShaderModule en un array
VkPipelineShaderStageCreateInfo.VkRayTracingShaderGroupCreateInfoKHR.
Cada elemento se convertirá al final en una entrada de la Shader Binding
Table.vkCreateRayTracingPipelineKHR.vkGetRayTracingShaderGroupHandlesKHR.VK_BUFFER_USAGE_SHADER_BINDING_TABLE_BIT_KHR y copiar los
handlers.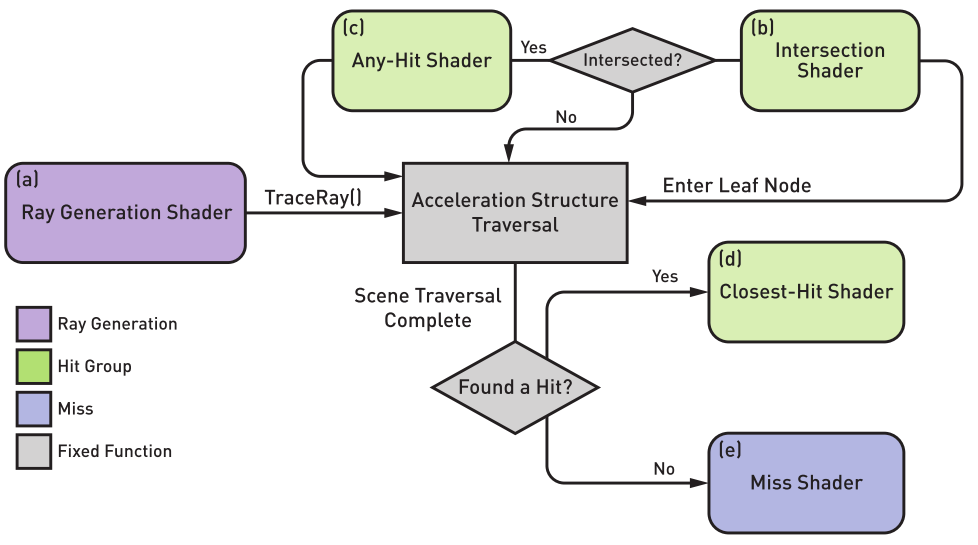
Cada entrada de la SBT contiene un handler y una serie de parámetros embebidos. A esto se le conoce como Shader Record. Estos records se clasifican en:
Una de las partes más difíciles de la SBT es saber cómo se relacionan record y geometría. Es decir, cuando un rayo impacta en una geometría, ¿a qué record de la SBT llamamos? Esto se determina mediante los parámetros de la instancia, la llamada a trace rays, y el orden de la geometría en la BLAS.
Para conocer a fondo cómo funciona la Shader Binding Table, puedes visitar (Usher 2021, 193) o (Usher 2019).
El código de la creación de la pipeline está encapsulado en la
función Engine::createRtPipeline(), que se puede consultar
en el archivo
application/vulkan_ray_tracing/src/engine.cpp.
En esencia, este método realiza las siguientes tareas:
VkPipelineShaderStageCreateInfo
para almacenar la información de cada fase..spv en la
estructura junto con sus parámetros correctos.El formato de materiales y objetos usados es el
Wavefront (.obj). Aunque es un sistema
relativamente antiguo y sencillo, se han usado definiciones específicas
en los materiales para adaptarlo a Physically Based Rendering.
Entre los parámetros del archivo de materiales .mtl,
destacan:
Todos estos parámetros son opcionales y se pueden omitir, pero lo normal es incluir los tres primeros (\(K_a\), \(K_d\), \(K_s\)).
// host_device.h
struct WaveFrontMaterial
{
vec3 ambient;
vec3 diffuse;
vec3 specular;
vec3 transmittance;
vec3 emission;
float shininess;
float ior;
float dissolve;
int illum;
int textureId;
};Existe un parámetro adicional llamado illum. Controla el
modelo de iluminación usado. Nosotros lo usaremos para distinguir tipos
diferentes de materiales. Los códigos representan lo siguiente:
| Modelo | Color | Reflejos | Transparencias |
|---|---|---|---|
0 |
Difusa | No | No |
1 |
Difusa, ambiental | No | No |
2 |
Difusa, especular, ambiental | No | No |
3 |
Difusa, especular, ambiental | Ray traced | No |
4 |
Difusa, especular, ambiental | Ray traced | Cristal |
5 |
Difusa, especular, ambiental | Ray traced (Fresnel) | No |
6 |
Difusa, especular, ambiental | Ray traced | Refracción |
7 |
Difusa, especular, ambiental | Ray traced (Fresnel) | Refracción |
8 |
Difusa, especular, ambiental | Sí | No |
9 |
Difusa, especular, ambiental | Sí | Cristal |
10 |
Puede arrojar sombras a superficies invisibles. |
La última estructura de datos importante que debemos estudiar es la utilizada para las fuentes de luz. Desafortunadamente, en este trabajo no se ha implementado una abstracción sólida.
Se ha reaprovechado la definición del rasterizador por defecto para que tanto el path tracer como el anterior utilicen fácilmente iluminación estática.
La idea básica es que, en vez de depender de los elementos de la escena para proporcionar luz, se conozca una fuente de iluminación en todo momento. Dicha fuente puede ser puntual o direccional, y puede ser controlada mediante la interfaz. El estado de la fuente se traspasa a los shaders mediante una push constant:
struct PushConstantRay
{
...
vec3 light_position;
float light_intensity;
int light_type;
};El parámetro light_intensity corresponde a la potencia
\(\Phi\), y el tipo
light_type puede ser 0 para puntual o
1 para direccional.
Claramente esta decisión técnica favocere facilidad de implementación en detrimento de flexibilidad, solidez y correctitud. Esta interfaz es una de las áreas de futura mejora, y haría falta una revisión considerable. Sin embargo, por el momento, funciona.
La implementación en los shaders es muy sencilla. Podemos usar lo aprendido en muestreo directo de fuentes de luz. En el closest hit, primero calculamos la información relativa a la posición y la intensidad de la luz:
vec3 L;
float light_intensity = pcRay.light_intensity;
float light_distance = 100000.0;
float pdf_light = 1; // prob. de escoger ese punto de la fuente de luz
float cos_theta_light = 1; // Ángulo entre la la dir. del rayo y luz.
if (pcRay.light_type == 0) { // Point light
vec3 L_dir = pcRay.light_position - world_position; // vector hacia la luz
light_distance = length(L_dir);
light_intensity = pcRay.light_intensity / (light_distance * light_distance);
L = normalize(L_dir);
// Solo tenemos un punto => pdf light = 1, cos_theta light = 1.
cos_theta_light = dot(L, world_normal);
}
else if (pcRay.light_type == 1) { // Directional light
L = normalize(pcRay.light_position);
cos_theta_light = dot(L, world_normal);
}Sin embargo, esto no es suficiente. Se nos olvida comprobar un detalle sumamente importante:
¿Se ve la fuente de luz desde el punto de intersección?
Si no es así, ¡no tiene sentido que calculemos la influencia luminaria de la fuente! La carne de burro no se transparenta, después de todo. A no ser que sea un toro hecho de algún material que presente transmitancia [40], en cuyo caso se debería refractar acordemente el rayo de luz.
Volviendo al tema: este tipo de problemas de oclusión se suelen resolver mediante algún tipo de test de visibilidad. El más habitual es usar shadow rays. En la preparación de la pipeline se fija este tipo de shaders junto a los del tipo miss:
// void Engine::createRtPipeline()
// ...
stage.module = nvvk::createShaderModule(m_device,
nvh::loadFile("spv/raytrace.rmiss.spv", true, defaultSearchPaths, true)
);
stage.stage = VK_SHADER_STAGE_MISS_BIT_KHR;
stages[eMiss] = stage;
// El segundo miss shader se invoca cuando un shadow ray no ha colisionado con la geometría.
// Simplemente, indica que no ha habido oclusión.
stage.module = nvvk::createShaderModule(m_device,
nvh::loadFile("spv/raytraceShadow.rmiss.spv", true, defaultSearchPaths, true
));
stage.stage = VK_SHADER_STAGE_MISS_BIT_KHR;
stages[eMiss2] = stage;
// Resto de shaders...La continuación del código quedaría de la siguiente forma:
if (dot(normal, L) > 0) {
// Preparar la invocación del shadow ray
float tMin = 0.001;
float tMax = light_distance;
vec3 origin = gl_WorldRayOriginEXT + gl_WorldRayDirectionEXT * gl_HitTEXT;
vec3 ray_dir = L;
uint flags = gl_RayFlagsSkipClosestHitShaderEXT;
prdShadow.is_hit = true;
prdShadow.seed = prd.seed;
traceRayEXT(topLevelAS,
flags, // rayFlags
0xFF, // cullMask
1, // sbtRecordOffset => invocar el shader de sombras
0, // sbtRecordStride
1, // missIndex
origin, // ray origin
tMin, // ray min range
ray_dir, // ray direction
tMax, // ray max range
1 // payload (location = 1)
);
float attenuation = 1;
if (!prdShadow.is_hit) {
hit_value = hit_value + light_intensity*BSDF*cos_theta_light / pdf_light;
}
else {
attenuation = 1.0 / (1.0 + light_distance);
}
}Y con esto, hemos conseguido añadir dos tipos de fuentes de iluminación.
Debemos destacar que el programa no conoce la posición de los objetos emisivos de la escena. Esto significa que no podemos muestrearlos explícitamente. En la comparativa comprobaremos cómo afecta esto a la calidad de imagen. Además, en la conclusión hablaremos de cómo se podría solventar este problema.
El código de la sección “Pseudocódigo de un path tracer” tiene el problema de que utiliza recursividad. En la implementación de los shaders, esto supondría generar rayos desde el closest hit. Para evitarlo, reestructuraremos el código de forma que únicamente se lancen desde el raygen y calculemos la radiancia total en dicho shader.
El código resultante sería el siguiente: por una parte, una función
se encarga de generar los rayos, denominada
pathtrace():
vec3 pathtrace(vec4 ray_origin, vec4 ray_dir, float t_min, float t_max, uint ray_flags) {
// Inicializar el payload correctamente
prd.depth = 0;
prd.hit_value = vec3(0);
prd.ray_origin = ray_origin.xyz;
prd.ray_dir = ray_dir.xyz;
prd.weight = vec3(0);
// prd.seed ya estaba inicializado
vec3 current_weight = vec3(1);
vec3 hit_value = vec3(0);
// Evitar llamadas recursivas a traceRayEXT() desde el closest hit.
for (; prd.depth < pcRay.max_depth; prd.depth++) {
traceRayEXT(topLevelAS, // acceleration structure
ray_flags, // rayFlags
0xFF, // cullMask
0, // sbtRecordOffset
0, // sbtRecordStride
0, // missIndex
prd.ray_origin, // ray origin
t_min, // ray min range
prd.ray_dir, // ray direction
t_max, // ray max range
0 // payload (location = 0)
);
hit_value += prd.hit_value * current_weight;
current_weight *= prd.weight;
}
return hit_value;
}Y por otro lado, otra función debe almacenar correctamente la información del punto de impacto, así como la radiancia de ese punto. Corresponde al closest hit:
closest_hit() {
// Sacar información sobre el punto de impacto: material, normal...
WaveFrontMaterial mat = material(world_position);
// Preparar información para el raygen
prd.hit_value = material.emision;
prd.ray_origin = world_position;
prd.ray_dir = siguiente_direccion(material)
float probabilidad = pdf(prd.ray_dir);
// Calcular la radiancia
float cos_theta = dot(prd.ray_dir, normal);
vec3 BRDF = BRDF(material)
prd.weight = (BRDF * cos_theta) / pdf
return prd
}El código final es considerablemente más complejo que este que se presenta. Sin embargo, se han obviado algunos detalles de implementación con la intención de ser explicativo.
Esta versión no es tan intuitiva. ¿Por qué este último genera el mismo resultado que el de la versión recursiva?
Analicemos lo está ocurriendo.
Sea \(h\) el hit value (que simboliza la radiancia), \(w\) el peso, \(f_i\) la BRDF (o en su defecto, BTDF/BSDF), \(i\), \(e_i\) la emisión, \(\cos\theta_i\) el coseno del ángulo que forman la nueva dirección del rayo y la normal, y \(p_i\) la función de densidad que, dada una dirección, proporciona la probabilidad de que se escoja. El subíndice denota el \(i\)-ésimo punto de impacto.
En esencia, este algoritmo está descomponiendo lo que recogemos en
weight, que es \(f_i \cos\theta_i
/ p_i\). Inicialmente, para el primer envío del rayo, \(h = (0, 0, 0)\), \(w = (1, 1, 1)\). Tras trazar el primer
rayo, se tiene que
\[ \begin{aligned} h & = 0 + e_1 w = e_1, \\ w & = \frac{f_1 \cos\theta_1}{p_1} \end{aligned} \]
Tras el segundo rayo, obtenemos
\[ \begin{aligned} h & = e_1 + e_2 w = \\ & = e_1 + e_2 \frac{f_1 \cos\theta_1}{p_1}, \\ w & = \frac{f_1 \cos\theta_1}{p_1} \frac{f_2 \cos\theta_2}{p_2} \end{aligned} \]
Y para el tercero
\[ \begin{aligned} h & = e_1 + e_2 \frac{f_1 \cos\theta_1}{p_1} + e_3 w = \\ & = e_1 + e_2 \frac{f_1 \cos\theta_1}{p_1} + e_3 \frac{f_1 \cos\theta_1}{p_1} \frac{f_2 \cos\theta_2}{p_2} = \\ & = e_1 + \frac{f_1 \cos\theta_1}{p_1}\textcolor{verde-oscurisimo}{\left(e_2 + e_3 \frac{f_2 \cos\theta_2}{p_2}\right)}, \\ w & = \frac{f_1 \cos\theta_1}{p_1} \frac{f_2 \cos\theta_2}{p_2} \frac{f_3 \cos\theta_3}{p_3} \end{aligned} \]
El \(\textcolor{verde-oscurisimo}{\text{término que acompaña}}\) a \(\frac{f_1 \cos\theta_1}{p_1}\) es la radiancia del tercer punto de impacto. Por tanto, a la larga, se tendrá que \(h\) estima correctamente la radiancia de un punto. Con esto, podemos afirmar que
\[ h \approx \frac{1}{N} \sum_{j = 1}^{N}{\frac{f(p, \omega_o \leftarrow \omega_j) L_i(p, \omega_j) \cos\theta_j}{P\left[ \omega_j \right]}} \]
Este algoritmo supone una mejora de hasta 3 veces mayor rendimiento que el recursivo (NVIDIA 2022a, glTF Scene).
Normalmente, mandamos los rayos desde el centro de un pixel. Podemos conseguir una mejora sustancial de la calidad con un pequeño truco: en vez de generarlos siempre desde el mismo sitio, le aplicamos una pequeña perturbación (jittering). Así, tendremos una variación de colores para un mismo pixel, por lo que podemos hacer una ponderación de todos ellos. A este proceso lo que llamamos supersampling mediante jittering.
Si conforme pasa el tiempo utilizamos la información de las imágenes anteriores para renderizar el frame actual, podemos conseguir un resultado aún mejor que aplicando solo supersampling. Es decir, promediando el color de los últimos \(N\) frames para generar el frame actual. Esta técnica se llama acumulación temporal.
Es importante destacar que la acumulación temporal solo es válido cuando la cámara se queda estática. Al cambiar de posición, la información del píxel se ve alterada significativamente, por lo que debemos reconstruir las muestras desde el principio7.
La implementación es muy sencilla. Está basada en el tutorial de (NVIDIA 2022a, jitter camera). Debemos modificar tanto el motor como los shaders para llevar el recuento del número de frames en las push constants.
Definimos el número máximo de frames que se pueden acumular:
// engine.h
class Engine {
//...
int m_maxAcumFrames {100};
}Las push constant deberán llevar un registro del frame en el que se encuentran, así como un número máximo de muestras a acumular para un pixel:
// host_device.h
struct PushConstantRay {
//...
int frame;
int nb_samples
}El número de frame se reseteará cuando la cámara se mueva, la ventana se reescale, o se produzca algún efecto similar en la aplicación.
Finalmente, en los shaders podemos implementar lo siguiente:
// raytrace.rgen
vec3 pixel_color = vec3(0);
for (int smpl = 0; smpl < pcRay.nb_samples; smpl++) {
pixel_color += sample_pixel(image_coords, image_res);
}
pixel_color = pixel_color / pcRay.nb_samples;
if (pcRay.frame > 0) {
vec3 old_color = imageLoad(image, image_coords).xyz;
vec3 new_result = mix(
old_color,
pixel_color,
1.f / float(pcRay.frame + 1)
);
imageStore(image, image_coords, vec4(new_result, 1.f));
}
else {
imageStore(image, image_coords, vec4(pixel_color, 1.0));
}// pathtrace.glsl
vec3 sample_pixel() {
float r1 = rnd(prd.seed);
float r2 = rnd(prd.seed);
// Subpixel jitter: mandar el rayo desde una pequeña perturbación del pixel para aplicar antialiasing
vec2 subpixel_jitter = pcRay.frame == 0
? vec2(0.5f, 0.5f)
: vec2(r1, r2);
const vec2 pixelCenter = vec2(image_coords.xy) + subpixel_jitter;
// ...
vec3 radiance = pathtrace(rayo);
}En la sección de la comparativa estudiaremos a fondo los efectos de esta técnica.
Con el código de la sección anterior, existe un problema con los colores finales. El algoritmo de pathtracing no limita el máximo valor que puede tomar un camino. Sin embargo, Vulkan espera que la terna RGB provista esté en \([0, 1]^3\). Esto implica que los colores acabarán quemados.

Podemos corregir este problema mediante la acotación máxima de la terna RGB producida por el algoritmo. Sin embargo, esto ocasiona que la proporción de valores finales no sea correcta. Por ejemplo, si un camino genera la terna \(c = (15, 5, 7)\), el resultado de \(\max{(1, c_i)}, i = 1, 2, 3\) sería \((1, 1, 1)\).
Podemos corregir este problema mediante corrección de gamma. Esta es una operación no lineal utilizada en fotografía para corregir la luminacia, con el fin de compensar la percepción no lineal del brillo por parte de los humanos. En este caso, lo haremos al estilo (Shirley 2020a): tras tomar las muestras, aplicaremos una corrección para \(\gamma = 2.2\), lo cual implica elevar cada componente del píxel a la potencia \(\frac{1}{2.2}\); es decir, \((r_f, g_f, b_f) = (r^{\frac{1}{2.2}}, g^{\frac{1}{2.2}}, b^{\frac{1}{2.2}})\).
Tras esto, limitaremos el valor máximo de cada componente a 1 con la operación \(clamp()\).
vec3 pixel_color = vec3(0);
for (int smpl = 0; smpl < pcRay.nb_samples; smpl++) {
pixel_color += sample_pixel(image_coords, image_res);
}
pixel_color = pixel_color / pcRay.nb_samples;
if (USE_GAMMA_CORRECTION == 1) {
pixel_color = pow(pixel_color, vec3(1.0 / 2.2)); // Gamma correction for 2.2
pixel_color = clamp(pixel_color, 0.0, 1.0);
}
Espera. Esa no parece la misma escena. ¿No han cambiado los colores demasiado?
¡Bien visto! Es cierto que los colores se ven significativamente alterados. Esto es debido a la conversión de un espacio lineal de respuesta de radiancia a uno logarítmico. Algunos autores como Íñigo Quílez (coautor de la página Shader Toy) prefieren asumir esta deficiencia, y modificar los materiales acordemente a esto (Quílez 2013, The Color Space).
Nosotros no nos preocuparemos especialmente por esto. Este no es un trabajo sobre teoría del color, aunque nos metamos en varias partes en ella. El área de tone mapping es extensa y merecería su propio estudio.
Es importante mencionar que sin acumulación temporal, el código anterior produciría variaciones significativas para pequeños movimientos. Hay otras formas de compensarlo, como dividir por el valor promedio de las muestras más brillantes. Nosotros hemos optado por mezclar los píxeles generados a lo largo del tiempo.
En este capítulo vamos a analizar el resultado final del proyecto. Estudiaremos cómo se ve el motor, cómo rinde en términos de tiempo de procesado de un frame, y compararemos las imágenes producidas con otras similares; tanto producidas por otros motores, como situaciones en la vida real.
Una vez se ha compilado el
proyecto, puedes encontrar el ejecutable en
./application/bin_x64/Debug. Abre el binario para entrar en
el programa.

Si alguna vez has usado un motor de renderización en 3D (como Blender, Unity, Unreal Engine o AutoCAD), el comportamiento debería resultarte familiar. El uso de nuestro progama es muy similar al de los anteriores:
La interfaz permite cambiar parámetros de diversos tipos. Enumeremos algunas de las opciones:
(0.808, 0.839, 0.878)) y deshabilitar el modo ray
tracing.extras se puede modificar el modo de
navegación (Examine, Fly o Walk
como comentábamos anteriormente), la distancia de renderizado y la
velocidad de movimiento.Para ocultar la interfaz gráfica, pulsa F10.
El programa viene acompañado de varios mapas. Desafortunadamente, para cambiar de escena es necesario recompilar el programa. Las instrucciones necesarias para conseguirlo son las siguientes:
load_scene(Scene::escena, engine);
que se encuentra en el archivo main.cpp.Scene::escena por alguna entrada del enumerado
Scene. Puedes encontrar sus posiblidades en el archivo
Scenes.hpp.Se puede ver la lista de escenas disponibles en la tabla [5.1]
| Nombre de escena | Descripción | Imagen |
|---|---|---|
cube_default |
La escena por defecto del programa. Muestra un simple cubo. |  |
any_hit |
Desmostración de las capacidades del shader anyhit. |  |
cube_ reflective |
Ejemplifica ray traced reflections. |  |
medieval _building |
Una sencilla escena que contiene una casa medieval con texturas. |  |
cubes |
Dos cubos de diferente material sobre un plano reflectante. |  |
cornell_box _original |
Una reconstrucción de la caja de Cornell original (“Photograhic images of the cornell box” 2005). |  |
cornell_box _mirror |
Similar a la caja original, esta escena es una recreación de (“Cornell box comparison” 1998). |  |
cornell_box _esferas |
Una caja de Cornell con esferas. Se puede comparar con (Jensen 2001, 107 fig. 9.10). |  |
cornell_box _saturada |
Otra caja de Cornell similar a la original, pero con las paredes saturadas. |  |
cornell_box _glossy |
En esta caja se encuentran dos esferas de diferente material. Se puede comparar con (Jensen 1996, 17, fig. 6) |  |
cornell_box _iow |
La última caja de Cornell implementada en (Shirley 2020c). |  |
cornell_box _vacia |
La caja original sin las cajitas pequeñas dentro. |  |
cornell_box _vacia_an |
Similar a la anterior, pero con las paredes naranjas y azules. |  |
cornell_box _blanca |
Una caja vacía. Es un benchmark infernal para el ruido generado por la iluminación global. |  |
Ten en cuenta que las imágenes de las escenas no son definitivas. Están sujetas a cambios, pues los shaders todavía se encuentran en desarrollo.
A lo largo de este trabajo hemos visto una gran variedad de conceptos desde el punto de vista teórico. Ahora es el momento de ponerlo en práctica.
Empecemos por materiales. Se han implementado unos cuantos tipos diferentes, los cuales veremos ilustrados a continuación.
Los más simples son los difusos. La caja de Cornell original contiene dos objetos de este tipo:

Los materiales especulares glossy han sido modificados ligeramente para simular el parámetro de roughness de los metales, para compararlos con los de (Shirley 2020a):

Si hay algo en lo que destaca ray tracing, es en la simulación de espejos. En rasterización debemos recurrir a técnicas específicas como reflejos planares o cubemaps. Ray tracing solventa el problema con elegancia:

En la siguiente escena observamos dos esferas: una que presenta refracción y otra que no. Ambas utilizan las ecuaciones de Fresnel para modelar el comportamiento de la luz.

Los materiales transparentes los gestiona el shader anyhit. Permite descartar las intersecciones con aquellos objetos transparentes para permitir pasar algunos rayos:

En la primera versión del motor, se han implementado dos tipos de fuentes de luces: puntuales y direccionales.
Las fuentes de luz puntuales (spotlights en inglés) emiten luz alrededor suya, como si de pequeños soles se trataran. La figura [41] muestra cómo se comportan en la caja de Cornell original.

Por otro lado, las luces direccionales: imitan la luz proporcionada por algún objeto infinitamente lejano. Puedes ver un ejemplo en la figura [42].

Como las puntuales se comportan de manera muy similar en la caja de Cornell, podemos referirnos a la escena del edificio medieval para ver una diferencia más sustancial [43, 44]. En este caso, se aprecia el radio de influencia de la luz puntual.

La iluminación global es un fenómeno físico referente a luz que proviene de todas direcciones. Es el efecto que propicia el rebote constante de los fotones emitidos por fuentes de luz hacia una escena, adquiriendo las propiedades de los materiales en los que rebotan.
Dicho de esta forma, es difícil imaginarse cómo se comporta en la vida real. Para ilustrarlo, tomemos dos fotografías que se asemejan a la caja de Cornell.
En la escena [45] observamos cómo la luz del sol entra desde la parte de la derecha, rebotando en todo el espacio. Notamos cómo la escena tiene una tonalidad natural y cálida. Sin embargo, esta impresión es fácilmente modificable si alteramos la forma de arrojar la luz. Cerrando la puerta (la cual no puede ser vista en la fotografía, pero se encuentra a la derecha y es idéntica al cristal), la iluminación cambia completamente [46].

Podemos observar cómo todos los materiales adquieren un tinte rojizo, debido a la influencia tanto difusa como especular de la pared de la izquierda. Objetos que antes eran blancos inmaculados se vuelven rojos, como el inodoro. Incluso aquellas zonas en sombra consiguen un color rojizo. Esto es debido a que los fotones rebotan en el cristal rojo cuando más energía tienen. De esta forma, en la siguiente dirección tomada, los rayos transportan esta propiedad al resto de materiales, los cuales se visualizan como una tonalidad roja.

Path tracing consigue este efecto de manera natural por diseño. Este es uno de sus mayores puntos fuertes, pero a la vez lo hace computacionalmente caro. Dado que la escena de [45] y [46] es, esencialmente, una caja de Cornell, deberíamos apreciar un efecto similar en nuestra escena, ¿verdad?
¡Así es! La figura [47] es muy similar a la [46]. Se pueden apreciar los mismos efectos en la caja izquierda, los cuales no ocurrían con tanta intensidad en la escena original [fig. 36]

Lo mismo ocurre cuando cambiamos el foco a la pared de la derecha. Al ser verde, tintará el resto de los materiales de dicho color [Figura 48].

Este efecto es esencial para proporcionar realismo a una imagen digital. Sin iluminación global, los motores presentan un aspecto que podríamos considerar videojueguil: imágenes planas, con sombras abruptas y un aire de falsedad al que nos hemos llegado a acostumbrar. Por ello se han implementado varias técnicas en rasterización para suplir este efecto. Destacan los lightmaps, la componente ambiental de los materiales, cubemaps, oclusión ambiental e iluminación indirecta basada en probes.
Para un vistazo más a fondo de la iluminación global, puedes referirte al vídeo de Alex Battaglia en (Digital Foundry 2021b), en el cual cubre diferentes formas de resolver este problema, tanto en el caso de ray tracing como en el de rasterización.
Path tracing es un algoritmo costoso. Teniendo en cuenta que tratamos de desarrollar una aplicación en tiempo real, debemos prestar especial atención al coste de renderizar un frame. En esta sección vamos a hacer una comparativa de las diferentes opciones que se han implementado en el motor, estudiando la relación calidad de imagen y rendimiento.
Utilizaremos principalmente dos escenas:
cornell_box_original y cornell_box_esferas.
Esto es debido a que ofrecen cierta complejidad y los materiales de los
objetos permiten estudiar los parámetros del motor.
Para los análisis del rendimiento, se ha utilizado un procesador
Intel i5 12600K, una tarjeta gráfica Nvidia
2070 Super con un ligero overclock a 1900MHz y
2x8GB DDR4 3200MHz de RAM. A no ser que se diga lo
contrario, todas las imágenes tienen una resolución de 1280 x 720. Con
el fin de realizar una comparación justa, se ha implementado un modo de
benchmarking que se puede activar en el archivo
globals.hpp.
La medición del framerate ha sido realizada mediante la combinación
de los programas Afterburner y RTSS, los cuales han tomado muestras a
una tasa de 10 veces/s. EL procesamiento del log se ha llevado
a cabo con los notebooks de Jupyter disponibles en la carpeta
./utilities del repositorio; en la cual también se
encuentran los ya mencionados logs.
El principal parámetro que podemos variar es el número de muestras por píxel. En un estimador de Monte Carlo [30], \(\hat{I}_N = \frac{1}{N} \sum_{i = 1}^{N}{f\left(X_i\right)}\), corresponde a \(N \in \mathbb{N}\).
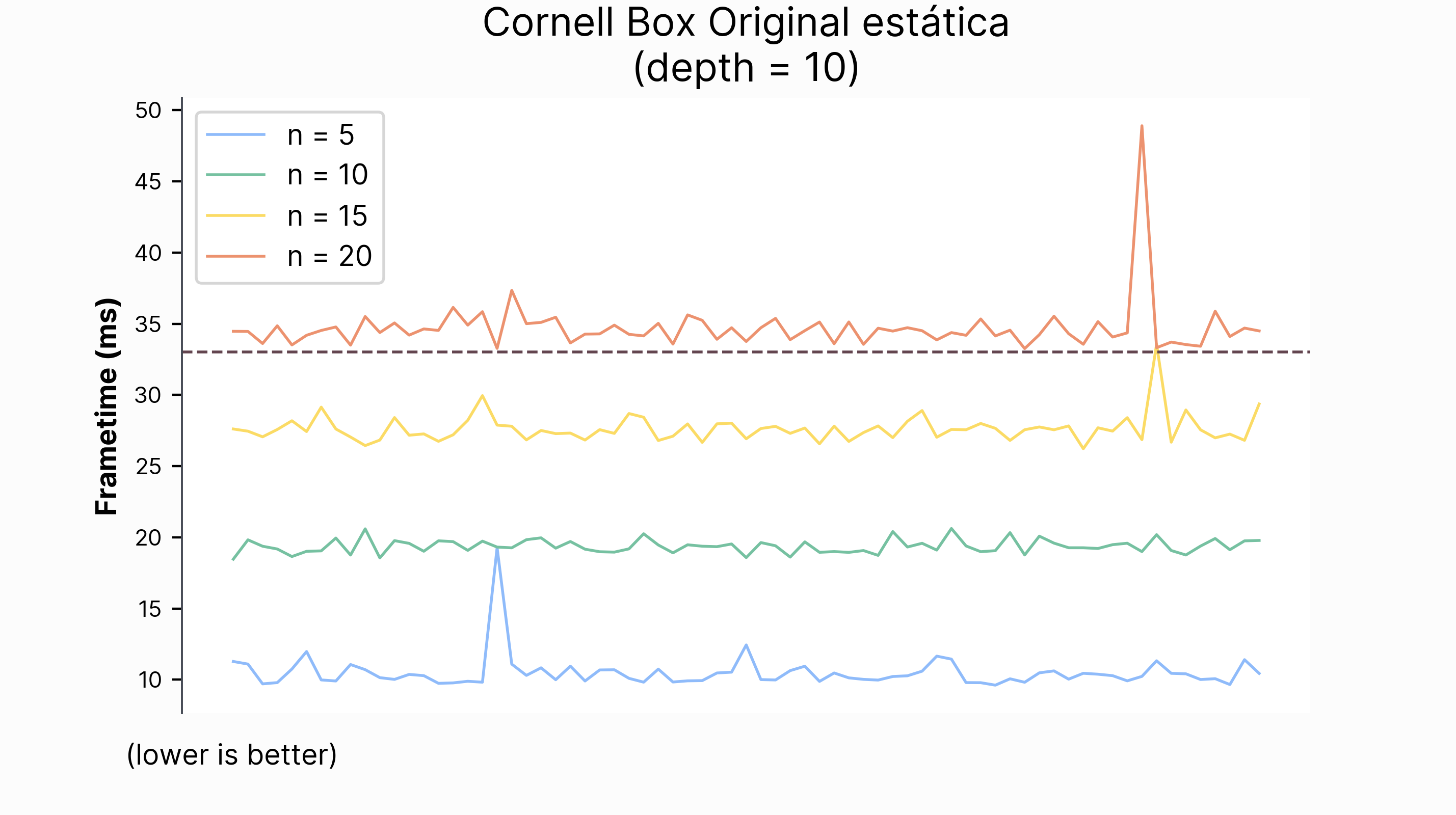
La figura [50] muestra cómo afecta al rendimiento el valor de \(N\). Vemos cómo un número bajo de muestras (alrededor de 5) produce un frametime de aproximadamente 12 milisegundos, lo cual corresponde a 83 frames por segundo. Duplicando \(N\) hasta las 10 muestras, produce un aumento del frametime hasta los 20 ms de media (50 FPS). Algo similar pasa con el resto de valores: 15 muestras suponen una media de 28 ms (35 FPS) y 20 muestras unos 35 ms (28 FPS). Sacamos en claro que, en esta escena, no debemos aumentar las muestras a un valor superior a 20, pues entraríamos en terreno de renderizado en diferido. No debemos superar la barrera de los 33 milisegundos, pues supondría una tasa de refresco de imagen inferior a los 30 FPS.
Podemos concluir que, en esta escena, el coste de una muestra por píxel es de aproximadamente 2 milisegundos en esta escena. Este valor puede ser hallado promediando el coste medio de cada frame en cada valor del parámetro.
No obstante, es importante mencionar que cada escena tiene un cierto sobrecoste particular. Generar la TLAS y la BLAS, así como la carga de objetos y materiales individuales ocupa tiempo de CPU, el cual es independiente a la generación de las muestras. Es decir, que existe una constante \(a\) para la cual se da la relación
\[ \text{tiempo de renderizado} \approx a + N t \text{ (milisegundos/frame)} \]
Donde \(N \in \mathbb{N}\) es el
número de muestras y \(t\) es el tiempo
medio que tarda en renderizarse un frame. Si bajamos el número
de muestras a uno en la escena cornell_box_original,
obtenemos que el frametime es de 2.64 ms/frame. Esto
nos dice que el coste de la escena es de aproximadamente 0.600
milisegundos.
El número de muestras tiene un grandísimo efecto en la calidad de
imagen. Volviendo a la escena anterior, podemos ver cómo cambia el ruido
al variar el parámetro samples. Para las siguientes
imágenes, se ha deshabilitado la acumulación temporal, pues en esencia,
proporcionaría un mayor número de muestras en el tiempo.
Con una única muestra por píxel, la imagen final aparece muy ruidosa. Aumentarlo a 5 mejora bastante la situación, pero sigue habiendo demasiado ruido [51]

De forma similar, aumentarlo a 10 y a 20 implica un aumento de la calidad visual significativa.

No obstante, el cambio de 10 a 20 no supone un salto tan grande como el de 1 a 5. Esto sugiere que debemos usar otras técnicas para reducir la varianza del estimador. ¡La fuerza bruta no es la solución!
Una de las decisiones que tenemos que tomar en el diseño del algoritmo es saber cuándo cortar un camino. Hay varias formas de hacerlo, aunque destacan principalmente dos: fijar un valor máximo de profundidad o la ruleta rusa.
Analicemos la primera opción, que es la que hemos implementado
nosotros. Para ello, usaremos a la escena
cornell_box_esferas, pues los materiales reflectivos y
refractantes de las esferas nos servirán de ayuda para estudiar el coste
de un camino.
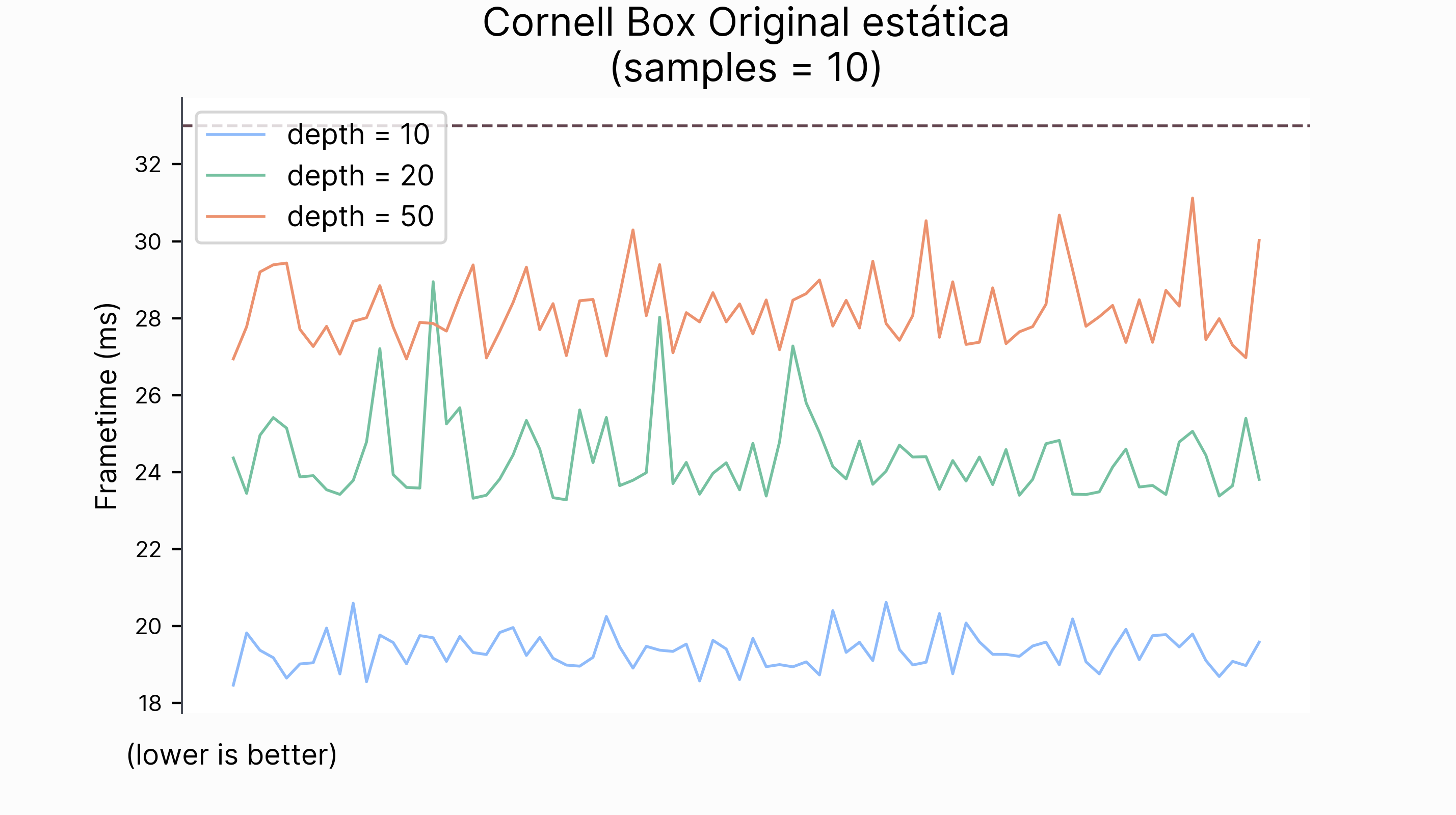
En esta figura [53] ocurre algo similar a [50]: como es evidente, aumentar la profundidad de un rayo aumenta el coste de renderizar un frame. Sin embargo, hay algunos matices que debemos estudiar con más detalle.
El primero es que cambiar la profundidad no es tan costoso como aumentar el número de muestras. Aún quintuplicando el valor por defecto de 10 rebotes a 50, vemos que el motor se mantiene por debajo de los 33 milisegundos. Para una profundidad de 10, el coste de un frame es de 19 milisegundos (52 FPS), mientras que para 50 es de 28 milisegundos (35 FPS). Tomando un valor intermedio de 20, el coste se vuelve de 24 milisegundos (41 FPS).
Llaman la atención las variaciones en el frametime conforme
aumenta la profundidad. Para un valor de depth = 10,
observamos que oscila entre los 18 y los 20 milisegundos. Sin embargo,
para los otros dos valores de 20 y 50 son habituales picos de varios
frames, llegando hasta los 5 milisegundos. Además, se aprecia
cierta inconsistencia. Sin embargo, esto no resulta un problema, pues la
oscilación media es de unos 3 milisegundos aproximadamente, lo cual
supone un decremento de unos 5 frames por segundo como
máximo.
La naturaleza de la escena afecta en gran medida al resultado. Por mera probabilidad, cuando un rayo rebota dentro de la caja, puede salir disparado hacia muchas direcciones. Destacarían en este caso dos situaciones:
La diferencia de rendimiento es sustancial. Pero, ¿merece la pena el coste adicional?.
Para responder a esta pregunta, primero debemos conocer cómo actúa este parámetro. Empezando con un número extremadamente bajo para los rebotes, vemos que parte de la escena ni siquiera se renderiza [54].

Aumentar el número de rebotes progresivamente permite que el camino adquiera mayor información. Con dos rebotes, permitimos que un camino adquiera información sobre la caja por dentro, así como un reflejo primitivo en las esferas [55].

Con 3 rebotes, la esfera izquierda refleja casi en su totalidad la esfera, pero vemos que el reflejo de la esfera derecha dentro de la izquierda está oscurecido [56].

Subiéndolo a 4 rebotes [57] se arregla mayoritariamente esto.

En esta escena, aumentar más allá de 5 o 6 rebotes produce una situación de retornos reducidos. La calidad de imagen no aumenta prácticamente nada, pero el coste se vuelve muy elevado [58, 59].


La acumulación temporal proporcionará una mejora enorme de la calidad visual sin perder rendimiento. Sin embargo, tiene como contrapartida que necesita dejar la cámara estática. Dependiendo de la situación esto podría ser un motivo factor no negociable, pero en nuestro caso, nos servirá.
Utilizando una única muestra, pero un valor de acumulación temporal de 100 frames máximos, proporciona una imagen sin apenas ruido [60].

Subiendo los parámetros a 200 frames de acumulación temporal y 10 muestras, se obtiene una imagen muy buena[61].

El tremendo efecto de esta técnica es debido a que actúa como normalización entre imágenes. Interpolando linealmente los resultados de diferentes frames, con el tiempo se conseguirá una foto de lo que se debe ver realmente, eliminando así el ruido y las luciérnagas.
Como se ha mencionado en la introducción, todas las escenas
anteriores se han renderizado a 720p. Podemos controlar la resolución
interna del motor desde el archivo globals.hpp. Veamos cómo
escala al variarla.
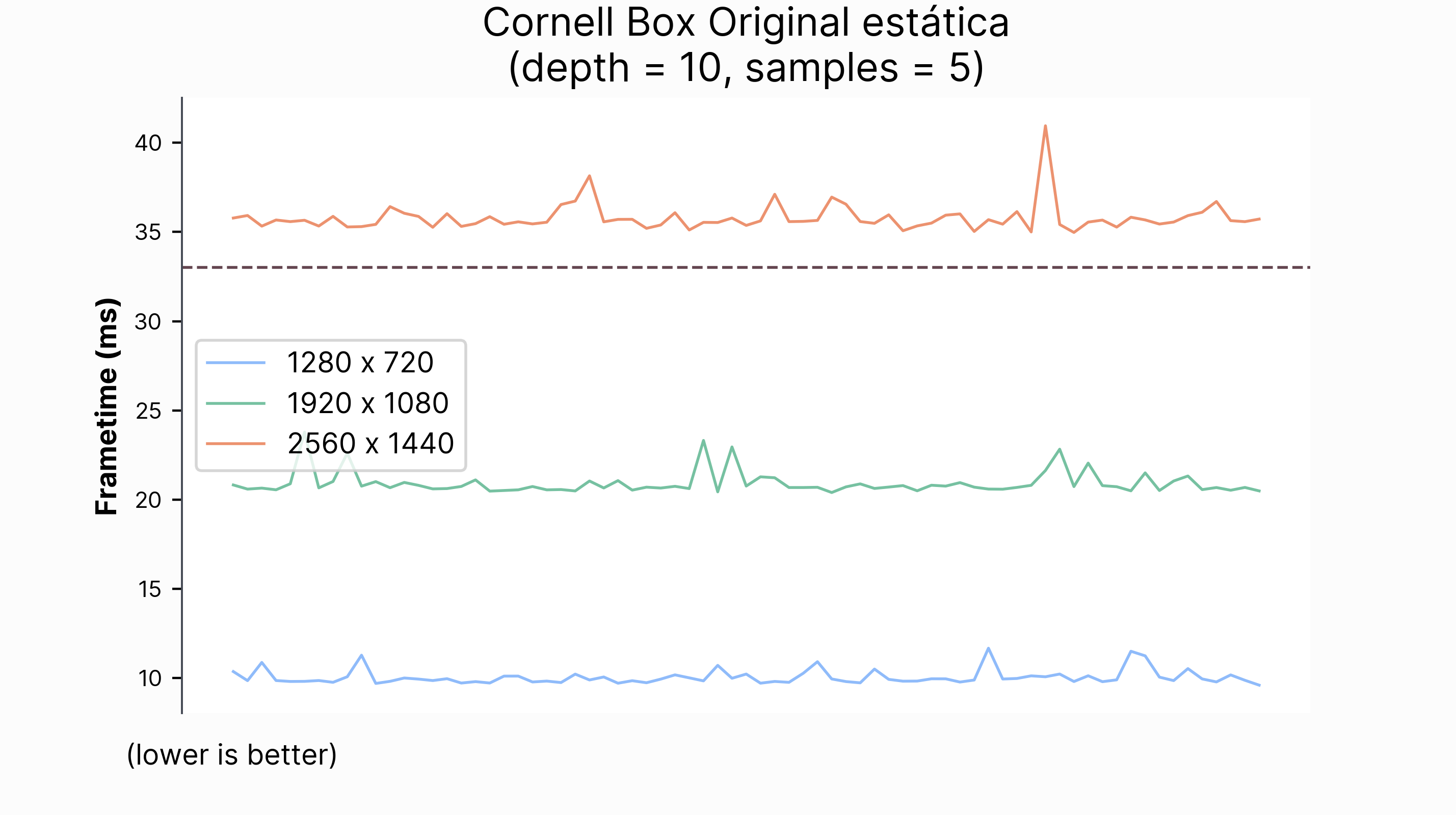
A 720p, la escena cornell_box_original corre a 105 FPS
(9.6 ms/frame), mientras que a 1080p, el motor corre a 47FPS
(21 ms/frame) y a 1440p, a 28 FPS (36 ms/frame). Como
vemos, la resolución tiene un gran impacto en el rendimiento. El cambio
de 720p a 1080p implica un aumento del 125% en el número de píxeles a
dibujar, por lo que es natural que el coste sea proporcional a esta
cantidad. 1440p tiene 1.7 veces más píxeles que 1080p.
En la práctica, ray tracing no suele utilizar resoluciones internas tan grandes. Se aplican otro tipo de técnicas para reducir el ruido, como veremos en el capítulo de estado del arte.
El muestreo por importancia consiste en tomar una función de densidad proporcional a la función a integrar para reducir la varianza. Se ha implementado muestreo por importancia para los materiales difusos. En particular, se ha utilizado dos estrategias diferentes para escoger direcciones aleatorias, que pueden observarse en la figura [63].

Para facilitar la comparativa, desde una posición estática se ha tomado una foto, y hemos ampliado la caja de la derecha digitalmente. De esta forma, podemos ver cómo la caja de la derecha contiene una menor cantidad de ruido, aún manteniendo los mismos parámetros de renderizado.
Con el fin de preparar este trabajo, se ha implementado la serie de libros de P. Shirley: In One Weekend (Shirley 2020a), The Next Week (Shirley 2020b) y The Rest of your Life (Shirley 2020c). Teniendo en cuenta que el producto final de esos libros es un offline renderer, sería interesante compararlo con nuestro motor que corre en tiempo real.
En esta sección enseñaremos escenas similares, mostraremos cuánto tarda en renderizar un frame en comparación a nuestro motor, y estudiaremos las diferencias en la calidad visual.
La implementación de los tres libros se encuentra en la carpeta
./RT_in_one_weekend del repositorio. Aunque el proyecto
presenta una gran complejidada por sí mismo, no comentaremos nada en
este trabajo. Sin embargo, comentaremos algunos detalles necesarios para
esta comparativa:
./RT_in_one_weekend/src/main.cpp. Los parámetros que se
pueden ajustar son el número de muestras
(samples_per_pixel), resolución de la imagen
(image_width) y profundidad del rayo
(max_depth)../RT_in_one_weekend/src/scenes.hpp.Es importante tener en mente que In One Weekend no está
optimizado. No está pensado para ser rápido; sino para ser
didáctico. Es por ello que el procesamiento está limitado a un
único hilo, y el renderizado se realiza únicamente por
CPU. Las imágenes que genera este motor utilizan el formato
.ppm y han sido reconvertidas a .png para este
trabajo.
Se ha implementado una escena específica para esta comparativa,
llamada cornell_box_iow. Es una situación análoga a la
última caja de Cornell del tercer libro. Para sacar las imágenes de In
One Weekend se han utilizado todas las técnicas vistas en los tres
libros, por lo que se espera que la calidad gráfica sea óptima. En
nuestra versión disponemos de prácticamente todos los métodos vistos en
este trabajo, variando diferentes parámetros con el fin de ver
resultados diferentes.
La siguiente tabla muestra una comparativa entre el coste de renderizar un frame en In One Weekend y en nuestro motor, usando una profundidad de 10 rebotes y una resolución de 720p:
| Número de muestras | In One Weekend (ms/frame) | Nuestra implementación (ms/frame) | Veces más rápido |
|---|---|---|---|
| 1 | 1032 |
2.6 |
\(\times\) 396.92 |
| 5 | 3934 |
11 |
\(\times\) 357.636 |
| 10 | 7459 |
20.4 |
\(\times\) 365.63 |
| 20 | 14516 |
39 |
\(\times\) 372.20 |
| 100 | 69573 |
~200 |
\(\times\) 347.87 |
| 1000 | 688388 |
~2000 |
\(\times\) 344.194 |
Como podemos observar, la diferencia es abismal. En el tiempo que tarda In One Weekend en producir una imagen con una única muestra, nuestro motor es capaz de generar una imagen de 500 muestras. Sin embargo, este resultado es esperable, pues a fin de cuentas, In One Weekend corre en la CPU con un único hilo, mientras que en nuestro motor se utilizan todos los recursos posibles.
Ahora bien, debemos hacernos una pregunta: ¿cómo es la calidad gráfica de cada uno?
Enfocaremos la respuesta desde dos puntos de vista diferentes: en el primero, nos fijaremos puramente en el número de muestras; y en el segundo, fijaremos un cierto margen de milisegundos por frame y comprobaremos el resultado en cada motor.
Comencemos la comparativa utilizando el número de muestras. Para las primeras imágenes fijaremos la acumulación temporal a un único frame. Explicaremos el motivo después.
Con una única muestra, se observa una diferencia enorme entre ambas versiones [64]. En nuestra implementación no se observa prácticamente nada. Solo somos capaces de distinguir la luz, un poco del reflejo de la caja izquierda y los caustics causados por la luz del techo. Mientras tanto, en In One Weekend, la imagen es ruidosa pero definida.

El motivo de esta diferencia es la forma de muestrear la escena. In One Weekend implementa muestreo directo de las fuentes de luz. Para conseguirlo, almacena la posición de la lámpara del techo, y en cada intersección muestrea un punto aleatorio de la fuente. En cambio, en nuestro motor, este tipo de fuentes no se muestrean directamente, sino que debemos contar con el azar para que aporten radiancia.
Una vez pasamos a 5 muestras [Figura 65], nuestro motor consigue una imagen más nítida, similar a la que In One Weekend genera con una muestra. En cambio, In One Weekend consigue un resultado muy bueno, aunque con muchas luciérnagas. Este fenómeno no ocurre en nuestra implementación por el tipo de muestreo.

Con 20 muestras nuestra implementación aún muestra un resultado algo ruidoso. ¿Se podría hacer algo para mejorarlo?

La respuesta es la acumulación temporal. Aunque, en esencia, la acumulación temporal es una forma de aumentar el número de muestras con respecto al tiempo, nuestra implementación utiliza interpolación para mezclar los colores de los frames. De esta forma, se consigue el efecto de normalización, lo cual elimina el ruido de la imagen con el tiempo. De esta forma conseguimos equiparar la imagen de ambas versiones [Figura 67].
Se puede observar cómo el tipo de ruido es diferente. En In One Weekend, el ruido se presenta en forma de píxeles blancos, debido a las luciérnagas generadas por el muestreo directo de la fuente de luz. En contrapartida, en nuestra implementación el ruido es negro debido a los rayos que no impactan en ninguna superficie tras rebotar.

Por último, subiendo el número de muestras a 1000 conseguimos una imagen muy nítida en ambas implementaciones [Figura 68]. Conseguimos apreciar una diferencia en los bordes de la esfera de la derecha, la cual seguramente se deba a un fallo en la implementación de la BRDF.

El presupuesto de tiempo (o frame budget en inglés) es la cantidad de milisegundos que disponemos para renderizar un frame. Este valor es importante cuando tratamos con aplicaciones en tiempo real. Por ejemplo, si queremos que nuestro motor corra a 60 imágenes por segundo, cada frame debe tardar un máximo de 16 milisegundos en ser generado. Una comparativa interesante sería fijar un valor para el tiempo, y ver qué calidad de imagen podemos conseguir con ambas implementaciones
Utilizando un presupuesto de 4000 milisegundos, In One Weekend es capaz de utilizar 5 muestras para la imagen, mientras que nuestro motor podría utilizar 10 muestras y 19 frames de acumulación temporal [Figura 69].
\[ 20.4 \frac{\text{ms}}{\text{10 muestras}} \cdot 19 \text{ frames de temp. acum.} = 3876 \text{ ms} \]

Como podemos observar, nuestra implementación consigue un resultado abismalmente mejor en el mismo periodo de tiempo.
Usando un valor mucho más alto de 70000 milisegundos, nuestra implementación se puede permitir utilizar 20 muestras y 1750 frames de acumulación temporal: \[ 40 \frac{\text{ms}}{\text{20 muestras}} \cdot 1750 \text{ frames de temp. acum.} = 70000 \text{ ms} \]
Esencialmente, la imagen que genera nuestra implementación es perfecta. No muestra ni un ápice de ruido; mientras que la de In One Weeekend presenta un resultado poco nítido [Figura 70].

Analizando las imágenes proporcionadas por ambos motores, podemos concluir que In One Weekend consigue un mejor resultado si nos basamos en el ruido de la imagen por número de muestras. Sin embargo, la rapidez de nuestro motor permite compensar los problemas de muestreo con un mayor número de muestras por milisegundo, lo cual le permite superar el resultado visual que In One Weekend consigue en un cierto periodo de tiempo.
No obstante, es importante recordar que ambas implementaciones tienen sus inconvenientes debido a la naturaleza de los respectivos trabajos, por lo que en ambos casos se podría mejorar el rendimiento. En el caso de In One Weekend, paralelizando el programa; y en el de nuestro motor, haciendo más robusto el muestreo directo de fuentes de luz.
Al inicio de este trabajo nos propusimos crear un motor de path tracing en tiempo real. Esta no era una tarea fácil, así que tuvimos que empezar desde las bases de la informática gráfica.
Primero estudiamos qué es exactamente el algoritmo path tracing, el cual es una forma de crear imágenes virtuales de entornos tridimensionales. Dado que es un método físicamente realista, necesitábamos comprender cómo se comporta la luz, con el fin de conocer de qué color pintar un píxel de nuestra imagen. Esencialmente, entendimos que los fotones emitidos por las fuentes de iluminación rebotan por los diferentes objetos de un entorno, adquiriendo partes de sus propiedades en el impacto.
No obstante, imitar a la realidad es una tarea titánica. Las ecuaciones radiométricas resultan computacionalmente complejas, por lo que no es posible crear una simulación perfecta de la luz. Por ese motivo recurrimos a las técnicas de Monte Carlo, las cuales utilizan sucesos aleatorios para estimar la cantidad de luz de un punto. Estos métodos hicieron viables ciertos cálculos necesarios para el algoritmo. Sin embargo, su naturaleza inexacta implica que existe un error de estimación. Esto nos hizo explorar algunas formas de reducir el ruido generado por las técnicas de integración de Monte Carlo, como el muestreo por importancia. En esencia, el muestreo por importancia es una mejor estrategia de muestreo que se adapta mejor a la distribución de los valores del integrando.
Una vez adquirimos el fundamento teórico, diseñamos un software que nos permitiera poner en práctica nuestros conocimientos. Escogimos la API gráfica Vulkan y un framework de Nvidia como base para el desarrollo. Debido a la complejidad del algoritmo tuvimos que construir numerosas abstracciones que aceleraran el proceso de renderizado, basándonos en tarjetas gráficas modernas. Aprender a programar en tarjetas gráficas no es sencillo, así que tuvimos que diseñar unos programas específicos de éstas llamados shaders; específicamente, los shaders de ray tracing.
Al final, obtuvimos el resultado deseado: un motor de path tracing capaz de producir imágenes de escenas virtuales.

Como en cualquier otro trabajo, durante el proceso de desarrollo tuvimos que algunas tomar decisiones técnicas que alteran la calidad del producto. Por ello, realizamos un análisis del rendimiento basándonos en el frame time –tiempo que tarda en un frame en renderizarse–, variando los parámetros de path tracing en el proceso. De esta forma, pudimos comprobar cuánto nos cuesta sacar imágenes de gran nitidez.
Finalmente, para poner en contexto el motor, comparamos nuestra implementación con el de otros autores. En este caso, con el path tracer de Peter Shirley creado en Ray Tracing In One Weekend (Shirley 2020a). Nos dimos cuenta de que, aunque nuestra versión genera las muestras de forma más tosca, la rapidez con la que rinde consigue compensar el ruido de la imagen, produciendo así resultados más nítidos.
Por todos estos motivos, podemos afirmar que el trabajo ha sido un éxito. Se han logrado todos los objetivos que nos propusimos de forma satisfactoria, y gracias a la naturaleza del proyecto, hemos podido observar los resultados gráficamente.
Crear un software de este calibre es una tarea de una complejidad enorme. Los motores de renderización requieren un equipo de desarrollo de un tamaño considerable, una gran inversión y un esfuerzo constante. Teniendo en cuenta el contexto del proyecto, en el camino ha sido necesario tomar decisiones imperfectas. En esta sección exploraremos algunas posibles mejoras para este trabajo.
La parte que más margen de mejora presenta es la interfaz de las fuentes de luz. En su estado actual, únicamente es posible utilizar dos tipos de fuentes externas a la escena: luces puntuales y direccionales, las cuales se muestrean de forma directa. Además, solo puede existir una única fuente de este tipo.
Este diseño propicia un error relacionado con la nitidez de la imagen. Una de las ideas clave de path tracing es generar muestras de forma inteligente: dado que calcular caminos es caro, tira rayos hacia zonas que aporten mucha información. En dichas zonas deben encontrarse, esencialmente, fuentes de luz. ¡Pero la interfaz no conoce dónde se encuentran los materiales emisivos de la escena! Eso implica que algunos rayos toman direcciones que no aportan nada. Esto lo pudimos comprobar empíricamente en la comparativa.
Otro tipo de interfaz que necesita una mejora sustancial es la de
materiales y objetos. En el estado actual del programa,
los elementos de la escena son cargados desde un fichero
.obj. Las propiedades del material son determinadas en el
momento del impacto de un rayo basándonos en los parámetros del archivo
de materiales asociado .mtl. Esta estrategia funciona
suficientemente bien en este caso, pues el ámbito de desarrollo es
bastante reducido.
Sin embargo, a la larga sería beneficioso reestructurar la carga y almacenamiento de los objetos. De esta forma, atacamos el problema anterior relacionado con los materiales emisivos, conseguiríamos mayor granularidad en los tipos de objetos y podríamos diseñar estrategias específicas para algunos tipos de materiales (como separar en diferentes capas de impacto los objetos transparentes). Esto también nos permitiría añadir nuevos tipos de materiales más fácilmente, como pueden ser objetos dieléctricos, plásticos, mezclas entre varios tipos, subsurface scattering…
Estas nuevas interfaces deberían ir acompañadas de una
refactorización de la clase Engine. El
framework que escogimos, nvpro-samples (NVIDIA 2022b), está destinado a ser
didáctico. Por tanto, el software presenta un alto acoplamiento. Separar
en varias clases más reducidas, como una clase para rasterización y otra
para ray tracing, sería esencial. Sin embargo, Vulkan es una API muy
compleja, por lo que requeriría de una gran cantidad de trabajo.
En este trabajo hemos implementado algunas técnicas de reducción de varianza del estimador de Monte Carlo para la ecuación del transporte de luz [23], lo cual permite reducir el ruido de la imagen final. Entre estas, se encuentran muestreo por importancia, next-event estimation o acumulación temporal de las muestras.
Sin embargo, existen numerosas técnicas que no se han desarrollado. Entre estas, se encuentran el uso de ruido como blue noise, muestreo por importancia múltiple, ruleta rusa o secuencias de baja discrepancia (métodos de quasi-Monte Carlo). Resultaría interesante ver cómo estas técnicas se comportan en comparación con las que sí hemos usado.
El siguiente nivel sería implementar algunas técnicas basadas en cadenas de Markov que vimos al final del capítulo de Monte Carlo. Destaca el algoritmo Metropolis-Hastings (Pharr, Jakob, and Humphreys 2016, Metropolis Light Transport). Este tipo de técnicas resultan complejas y se escapan del ámbito introductorio de este proyecto.
Como es evidente, nos hemos dejado muchos detalles en el tintero. Un aspecto que hubiera sido casi mandatorio desarrollar, pero que no se ha podido, es la capcacidad de hacer tests unitarios (lo que se conoce como Test Driven Development). Desafortunadamente los límites de tiempo no han permitido implementar este tipo de pruebas. Debido a la gran velocidad de desarrollo que ha sido requerida para sacar este proyecto adelante, integrar test unitarios hubiera supuesto una inversión de tiempo considerable.
Esto, evidentemente, es un gran problema. Hoy en día un software profesional requiere la comprobación de que el código funciona. En este caso, se podrían hacer algunas comprobaciones como el white furnace test. Aun así, integrar test en un ray tracer resulta algo más complicado que de costumbre teniendo en cuenta la naturaleza del programa.
Sería también conveniente aprender un sistema de debugging sólido. En el blog de (Galvan 2022c) se pueden encontrar algunas herramientras muy útiles para este propósito.
Después de un esfuerzo monumental como el que supone el desarrollo de un motor de renderizado es satisfactorio ver el resultado, y más sabiendo que tratamos con tecnología de última generación. Sin embargo, en el fondo, este trabajo no es más que un juguete. Mientras que este proyecto ha durado escasos meses, los profesionales llevan años trabajando en transporte de luz. Así que, ¡veamos qué se cuece en la industria!
En esta sección vamos a explorar ligeralmente el estado del arte. Veremos algunas de las técnicas que están cobrando fuerza en los últimos años, así como algunos motores profesionales. Le pondremos especial atención a cómo funciona el sistema de iluminación global de Unreal Engine 5, conocido como Lumen.
Durante el desarrollo del trabajo aprendimos que el número de muestras no lo es todo. De hecho, es una de las partes menos importantes. Para reducir el ruido de la imagen final, resulta muchísimo más eficiente diseñar una buena estrategia de muestreo.
Con los avances de ray tracing en tiempo real surgió una nueva rama del tratamiento de la computación gráfica conocida como denoising. Este proceso consiste en eliminar el ruido de la imagen final, y es una técnica que se puede aplicar a cualquier imagen.
A continuación, veremos una introducción a las técnicas modernas que se utilizan en ray tracing para acelerar la convergencia de rayos. Nos basaremos en las notas recogidas por Alain Galvan en su blog (Galvan 2022e) (Galvan 2022d) para enumerar algunas de las técnicas. Todas las referencias a los trabajos originales se encuentran recogidas en dicha entrada, por lo que recomiendo leerla para comprender mejor cada técnica.
Entre las técnicas basadas en muestreo que ya hemos estudiado se encuentran multiple importance sampling, next-event estimation, ruleta rusa y series de quasi-Monte Carlo.
Otro método muy común es el uso de ruido azul, o Blue Noise (Eric Heitz 2019). Este tipo de ruido proporcionan valores aleatorios por píxel para crear patrones de ruido. Lo bueno de este tipo de patrones es que pueden ser tratados con mayor facilidad que otros tipos de ruido. (Alan Wolfe 2021). Esto es debido a su distribución uniforme, que produce menos instancias de errores de alta frecuencia, lo cual hace que sean fáciles de difuminar y acumular (Galvan 2022e). El ruido azul puede ser creado eficientemente mediante generadores de secuencias cuasi-aleatorias como las de Sobol.

Del área del procesamiento de señales se han transferido filtros Gaussianos, medianos y guiados para promediar regiones de baja varianza. En los últimos años, una nueva variante de este tipo de técnicas ha surgido como consecuencia del machine learning, el cual estudiaremos más tarde.
Las técnicas de acumulación permiten reutilizar información anterior para suavizar el resultado final. Este tipo de técnicas empezaron originalmente en 1988 con irradiance caching (Greg Ward 1988).
Un método muy sencillo que hemos estudiado es la acumulación temporal, pero requiere que la cámara se quede estática. En la actualidad, los algoritmos más avanzados consiguen el mismo efecto con una cámara en movimiento. Para lograrlo, se requiere el uso de un motion buffer, el cual calcula el cambio en la posición de un vértice de un frame a otro. En la práctica suelen venir acompañados de motion vectors, los cuales también son usados para técnicas como temporal antialiasing (TAA) o temporal upscaling (Karis 2014) (TAA es una técnica de muestreo).
Algunos de los métodos más famosos son Spatio-Temporal Variance Guided Filter (SVGF), Spatial Denoising, Adaptive SVGF (A-SVGF) y Temporally dense ray tracing. Un algoritmo que se ha utilizado exitosamente en los últimos años es Spatiotemporal importance Resampling (ReSTIR) (Benedikt Bitterli 2020), el cual es capaz de procesar millones de luces dinámicas en tiempo real en alta calidad sin necesidad de introducir estructuras de datos excesivamente complejas. Está basado en el algoritmo Sampling Importance Resampling (STIR). Este último se puede estudiar a fondo en (Wolfe 2022)

Para cualquier persona que haya seguido el mundo de la tecnología en los últimos años, no debe resultarle sorprendente que machine learning haya influido en este campo. La industria de la tecnología está explorando su funcionamiento a fondo, y el transporte de luz se ha beneficiado de ello.
En la actualidad el propósito de las redes neuronales suele ser reconstruir la imagen desde una resolución considerablemente menor: en vez de renderizar una imagen a, por ejemplo, 4K, se computa primero a 1080p o menos y luego se reescala mediante inteligencia artificial. Las tecnologías más famosas que operan de esta manera son Nvidia Deep Learning Super Sampling (DLSS) (NVIDIA 2020a) e Intel XeSS (Intel 2022b). AMD lanzó recientemente FidelityFX Super Resolution 2.0 (FSR) (AMD 2022), pero no utiliza redes neuronales. Sin embargo, la consideraremos en esta sección, pues sus resultados son muy similares.
DLSS recibe imágenes a baja resolución y motion vectors, produciendo imágenes a alta resolución mediante un autoenconder convolucional. Los resultados son espectaculares, y consiguen un rendimiento mucho mayor que a resolución nativa sin perder calidad de imagen. En algunos casos, la reconstrucción acaba teniendo mayor nitidez que la imagen original, pues la red neuronal aplica antialiasing en el proceso.

Intel XeSS funciona de manera similar a DLSS, aunque todavía no se conocen los detalles. Su lanzamiento es extremadamente reciente, por lo que se están explorando los resultados. Se puede leer una entrevista realizada por Digital Foundry a los autores del proyecto en (Digital Foundry 2021c).
Los beneficios de estas técnicas son evidentes. Tal y como descubrimos en la comparativa, la resolución afecta en gran medida al rendimiento. Cuantos más píxeles tenga la imagen, mayor será el número de muestras que debamos tomar; y por lo tanto, mayor el coste de renderizar un frame. Bajando la resolución conseguimos una imagen con menos ruido pero poco apta para las pantallas de hoy en día. Haciendo super sampling solventamos este problema. Si la reconstrucción es de suficiente calidad, estaremos consiguiendo rendimiento superior a la resolución nativa.

Con la llegada de ray tracing en tiempo gracias a la arquitectura Turing en 2018, un mundo de nuevas posibilidades se abrió ante los ojos de la industria. La más beneficiada fue, sin lugar a dudas, la de los videojuegos debido a sus limitaciones del frame budget.
Es mandatorio que la imagen se produzca en un margen de tiempo muy reducido; como máximo, de 33 milisegundos. Teniendo en cuenta este estrechísimo margen, la mayor parte de las empresas se optó por una solución híbrida: en vez de utilizar ray tracing puramente, este algoritmo se reserva para ciertas partes de la pipeline de procesamiento. Entre estas se encuentran los reflejos y la iluminación global (Mihut 2020).
En vez de recaer en técnicas antiguas como reflejos en espacio de pantalla (screen-space reflections) se utiliza una forma reducida de ray tracing para computar estos efectos. En el proceso final de la pipeline híbrida de rasterización y ray tracing se combina el resultado de ambas técnicas para producir la imagen final.

Algunos productos comerciales que destacan por su uso de ray tracing híbrido son Ratchet & Clank: Rift Apart y Spiderman [Figura 76] de Insommiac Games, Cyberpunk 2077 de CD Project Red, Control de Remedy (Figura Digital Foundry 2020a).
No obstante, existen algunas implementaciones de motores que utilizan únicamente path tracing como algoritmo de renderizado. Entre estos, se cuentran Quake II RTX (NVIDIA 2018) o Minecraft RTX, del cual se puede encontrar un análisis técnico en el blog de (Galvan 2020). Los resultados gráficos son espectaculares, aunque se necesita un hardware gráfico considerablemente potente para poder correrlos.
Parte de la transición de la industria a ray tracing se debe a las capacidades de las consolas de la actual generación: Playstation 5 de Sony (“PlayStation 5” 2021), y Xbox Series X y Series S de Microsoft (“Xbox series x and series s” 2022). Ambas fueron lanzadas a finales del año 2020. Las dos consolas utilizan la arquitectura de AMD denominada RDNA 2 de AMD, la misma que se usa en sus gráficas de escritorio de última generación. PS5 empaqueta 36 unidades de cómputo (Compute Units, CUs), con una potencia de 10.23 TFLOPS para operaciones en coma flotante de 32 bits y 21.46 TFLOPS para las de 16. Por otra parte, Series X monta 52 CUs con una potencia teórica de 12.16 TFLOPS, mientras que Series S reduce el número de CUs a 20.
En verano de 2020 Mark Cerny habló sobre cómo se utilizaría las capacidades de la arquitectura en el futuro de la consola (Cerny 2020). Entre estos usos, destaca el audio, la iluminación global, las sombras, los reflejos e incluso ray puro.
Hace media década, el hecho de tener ray tracing en tiempo real en gráficas de consumidor parecía imposible; más aún en consolas. Resulta, por tanto, una evolución enorme en una industria que se ha convertido en una de las más importantes del mundo.
Unreal Engine 5 (Epic Games 2022a) es la última generación del Motor Unreal Engine creado por Epic Games. Es un software extremadamente complejo que empaqueta múltiples funciones, como animación, físicas, renderizado, audio, y un largo etcétera. Se usa tanto en la industria de la animación como en la de los videojuegos.
Una de las novedades de esta versión es la integración de un sistema de iluminación global, llamado Lumen. Junto a Nanite, que es un sistema de geometría virtualizada, es la caracaterística más importante que han presentado. Recientemente han detallado cómo funciona Lumen (Epic Games 2022b), así que estudiaremos qué técnicas han utilizado.

La iluminación global es el efecto que produce la luz cuando los fotones que la componen rebotan dentro de una escena. En el pasado (i.e., rasterización) se ha simulado mediante técnicas como lightmap baking, oclusión ambiental y similares. Sin embargo, como ya explicamos en secciones anteriores, estas técnicas presentan grandes limitaciones.
Lumen simula infinitos rebotes de la luz en una escena en tiempo real, actualizando la iluminación automáticamente Esto funciona tanto para interiores como exteriores, puesto que simula la luz proveniente del cielo. Además, el sistema tiene en cuenta materiales emisivos y la niebla volumétrica.

Como era de esperar, Lumen utiliza ray tracing para hacer el cálculo de la iluminación. Para conseguirlo, el sistema crea una versión simplificada de la escena en la cual resulta más fácil hacer intersecciones de rayos con objetos.
Por defecto se ha optado una forma de ray tracing basada en software, pues de esta manera se soporta más tipos de hardware. Se combinan Mesh Distance Fields [79] (mallas de polígonos que resultan eficientes a la hora de intersecar) mezcladas en un Global Distance Field en este tipo de ray tracing. No obstante, su versión de ray tracing basado en hardware es mandatoria para conseguir algunos efectos como reflejos especulares perfectos, pues de otra manera no se podrían conseguir en tiempo real.
Una optimización clave para que este sistema funcione de forma eficiente es el uso de surface caching. Trabajando en conjunto junto a Nanite, Lumen crea un atlas de texturas de aquellas mallas presentes alrededor del jugador de forma que se cubran las caras visibles desde algún punto de vista. Esto simplifica el coste de la evaluación del material.

Para el paso final del cálculo de la radiancia se usa un algoritmo basado en radiance caching presentado en (“Advances in real-time rendering in gaming courses” 2021). Como no resulta viable tirar rayos a diestro y siniestro por toda la escena, Lumen toma una pequeña porción de muestras y combina los cálculos de radiancia con información aportada por el material.

Otro punto clave del sistema es la elección de las direcciones que se van a trazar. Para escogerlas, se comprueba qué partes del último frame resultaron muy brillantes. Entonces, se mandan rayos hacia esas zonas, pues esto producirá resultados menos ruidos en este frame. Esta técnica la hemos estudiado, y se llama muestreo por importancia (de la luz entrante en este caso).
Este punto enlaza con nuestra comparativa con In One Weekend. Una de las conclusiones más interesantes que obtuvimos fue que utilizar muestreo por importancia de las fuentes de iluminación proporcionaba unos resultados considerablemente mejores que una estrategia de muestreo basada en direcciones aleatorias. Aunque en este caso no se muestrean las fuentes de luz, sí que se utilizan partes de la escena con mucha radiancia, por lo que el fundamento es el mismo.

Para calcular los reflejos de superficies se ha optado por promediar la radiancia de puntos en el mismo vecindario y acumulación temporal de frames para suavizar el resultado.

Finalmente, es importante destacar que las imágenes no son generadas a una gran resolución. Para conseguir una imagen digna de los tiempos actuales, los motores modernos utilizan una resolución interna cercana a 720p o 1080p que es escalada mediante algún método de upsampling. En este caso, se ha optado por Temporal Super Resolution, una técnica que comenzó con Unreal Engine 4 y ha evolucionado en esta versión. Su comportamiento es similar a DLSS o FSR.
Todas estas optimizaciones son esenciales para hacer que el motor corra en tiempo real. Aunque el rendimiento es extremadamente dependiente del tipo de contenido que se esté visualizando y los parámetros del sistema, Unreal Engine 5 puede correr a 60 FPS en consolas de la generación actual.
Cualquier proyecto de una envergadura considerable necesita ser planificado con antelación. En este capítulo vamos a hablar de cómo se ha gestionado este trabajo: mostraremos las herramientas usadas, influencias, los ciclos de desarrollo, el uso de integración continua, y compenetración entre documentación y path tracer
Antes de comenzar con la labor, primero uno se debe hacer una simple pregunta:
“Y esto, ¿por qué me importa?”
Dar una respuesta contundente a este tipo de cuestiones nunca es fácil. Sin embargo, sí que puedo proporcionar motivos por los que he querido escribir sobre ray tracing.
Una de las principales inspiraciones del proyecto ha sido (Digital Foundry 2022a). Este grupo de divulgación se dedica al estudio de las técnicas utilizadas en el mundo de los videojuegos. El inicio de la era del ray tracing en tiempo real les llevó a dedicar una serie de vídeos y artículos a esta tecnología, y a las diferentes maneras en las que se ha implementado. Se puede ver un ejemplo en (Digital Foundry 2020b).
Dado que esta área combina tanto informática, matemáticas y una visión artística, ¿por qué no explorarlo a fondo?
Ahora que se ha decidido el tema, es hora de ver cómo atacarlo.
Soy un fiel creyente del aprendizaje mediante la exploración. Conceptos que resulten tangibles, que se pueda jugar con ellos. Páginas como Explorable Explanations (Ncase 2022), el blog de (Ciechanowski 2022), el proyecto The napkin (Chen 2022) o el divulgador 3Blue1Brown (Sanderson 2022) repercuten inevitablemente en la manera en la que te planteas cómo comunicar textos científicos. Por ello, aunque esto no deja de ser un mero trabajo de fin de grado de una carrera, quería ver hasta dónde era capaz de llevarlo.
Otro punto importante es la manera de escribir. No me gusta especialmente la escritura formal. Prefiero ser distendido. Por suerte, parece que el mundo científico se está volviendo más familiar (Nature 2016), una tendencia a la que yo me he sumado. Además, la estructura clásica de un escrito matemático de “teorema, lema, demostración, corolario” no me agrada especialmente. He intentado preservar su estructura, pero sin ser tan explícito. Durante esta memoria he intentado introducir cada concepto de la manera más natural posible, y que las demostraciones se integren con el desarrollo.
Estos dos puntos, en conjunto, suponen un balance entre formalidad y distensión difícil de mantener.
Este proyecto está compuesto por 2 grandes pilares: documentación –lo que estás leyendo, ya sea en PDF o en la web– y software. Podemos distinguir varias fases en la planificación del proyecto, que quedan resumidas en el diagrama de Gantt [Figuras 83, 84]
Para comenzar, durante el verano de 2021 se implementarían los tres libros de Shirley de la “serie In One Weekend”: In One Weekend (Shirley 2020a), The Next Week (Shirley 2020b), y The Rest of your Life (Shirley 2020c). De esta forma, asentaríamos las bases del proyecto, acelerando así el aprendizaje.
Tras esto, comenzaría a desarrollarse el motor por GPU. Cuando se consiguiera una base sólida, se empezaría a alternar entre escritura de la memoria y el software. Es importante documentar lo que se realiza, pues no se puede implementar algo que no se entiende.
Sin embargo, esto era únicamente una planificación. Como todos sabemos, en la práctica los planes no suelen salir a la perfección. ¿Ha sido este un caso de una preparación desastrosa?
Por fortuna, la idea inicial se ha asemejado mucho a la realidad. Algunas fases han sido más rápidas que otras, mientras que otras partes han costado más trabajo. Los commits del repositorio ayudan a clasificar el tipo de trabajo, pero, en resumidas cuentas:
Con respecto a la metodología de trabajo que se ha seguido es podemos decir que es, esencialmente, una versión de Agile muy laxa (Beck et al. 2001). Apoyándonos en las herramientas ofrecidas por Github, diseñamos un sistema de requisitos mediante issues, tanto para la memoria como para el software. Más adelante veremos más a fondo cómo esta herramienta ha facilitado enormemente el desarrollo.
A la hora de desarrollar un proyecto de software, es importante realizar una estimación del coste del trabajo. En otro caso, se corre el riesgo de que no se pueda llegar a cumplir el objetivo. En este caso, el proyecto ha tenido un coste de 10314 €, que puede desglosarse de la siguiente manera:
El diseño gráfico juega un papel fundamental en este proyecto. Todos los elementos visuales han sido escogidos con cuidado, de forma que se logre un equilibrio entre la profesionalidad y la distensión. Esta identidad visual se extiende a todos los aspectos del trabajo.
Para la documentación en versión PDF, usamos como base la plantilla Eisvogel, de (Wagler 2022). Uno de sus puntos fuertes es la personalización, la cual aprovecharemos para darle un toque diferente.
La web utiliza como base el estilo generado por Pandoc, el microframework de CSS Bamboo de (Anh 2022) y unas modificaciones personales.
Un apartado al que se le debe prestar especial énfasis es a la combinación de tipografías. A fin de cuentas, nuestro objetivo es comunicar al lector nuevos conceptos de la manera más amigable posible. Escoger un tipo de letra correcto, aunque pueda parecer irrelevante a priori, facilitará la compresión de estas nociones.
Para este trabajo, se han escogido las siguientes tipografías:
Todas estas fuentes permiten un uso no comercial gratuito.

A fin de mantener consistencia, se ha creado una paleta de colores específica.

El principal objetivo es transmitir tranquilidad, pero a la misma vez, profesionalidad. De nuevo, buscamos la idea de profesionalidad distendida que ya hemos repetido un par de veces.
Partiendo del rojo que traía Eisvogel (lo que para nosotros sería el
rojo primario), se han creado el resto. En principio, con 5 tonalidades
diferentes nos basta. Todas ellas vienen acompañadas de sus respectivas
variaciones oscuras, muy oscuras, claras y muy claras. Corresponderían a
los color-100, color-300, color-500, color-700, color-900
que estamos acostumbrados en diseño web. Para la escala de grises, se
han escogido 7 colores en vez de 9. Son más que suficientes para lo que
necesitamos. Puedes encontrar las definiciones en el fichero de estilos,
ubicado en ./docs/headers/style.css.
Todos los colores que puedes ver en este documento se han extraído de la paleta. ¡La consistencia es clave!
Encontrar una herramienta que se adapte a un workflow es complicado. Aunque hay muchos programas maravilosos, debemos hacerlos funcionar en conjunto. En este apartado, vamos a describir cuáles son las que hemos usado.
Principalmente destacan tres de ellas: Github, Pandoc y Figma. La primera tendrá su propia sección, así que hablaremos de las otras.
Pandoc (MacFarlane 2021) es una herramienta estupendísima de conversión de documentos. Se puede usar para convertir un tipo de archivo a otro. En este caso, se usa para convertir una serie de ficheros Markdown (los capítulos) a un fichero HTML (la web) y a PDF. Su punto más fuerte es que permite escribir LaTeX de forma simplificada, como si se tratara de sugar syntax. Combina la simplicidad de Markdown y la correctitud de LaTeX.
Su funcionamiento en este proyecto es el siguiente: Primero, recoge
los capítulos que se encuentra en docs/chapters, usando una
serie de cabeceras en YAML que especifican ciertos parámetros (como
autor, fecha, título, etc.), así como scripts de Lua. Estas caceberas se
encuentran en docs/headers. En particular:
meta.md recoge los parámetros base del trabajo.pdf.md y web.md contienen algunas
definiciones específicas de sus respectivos formatos. Por ejemplo, el
YAML del PDF asigna las variables disponibles de la plantilla Eisvogel;
mientras que para la web se incluyen las referencias a algunas
bibliotecas de Javascript necesarias o los estilos
(docs/headers/style.css, usando como base Bamboo.math.md contiene las definiciones de LaTeX.standard-code.lua formatea
correctamente los bloques de código para la web.Un fichero Makefile (docs/Makefile) contiene varias
órdenes para generar ambos formatos. Tienen varios parámetros
adicionales de por sí, como puede ser la bibliografía
(docs/chapters/bibliography.bib).
Figma (Figma 2022) es otro de esos programas que te hace preguntarte por qué es gratis. Es una aplicación web usada para diseño gráfico. Es muy potente, intuitiva, y genera unos resultados muy buenos en poco tiempo. Todos los diseños de este trabajo se han hecho con esta herramienta.
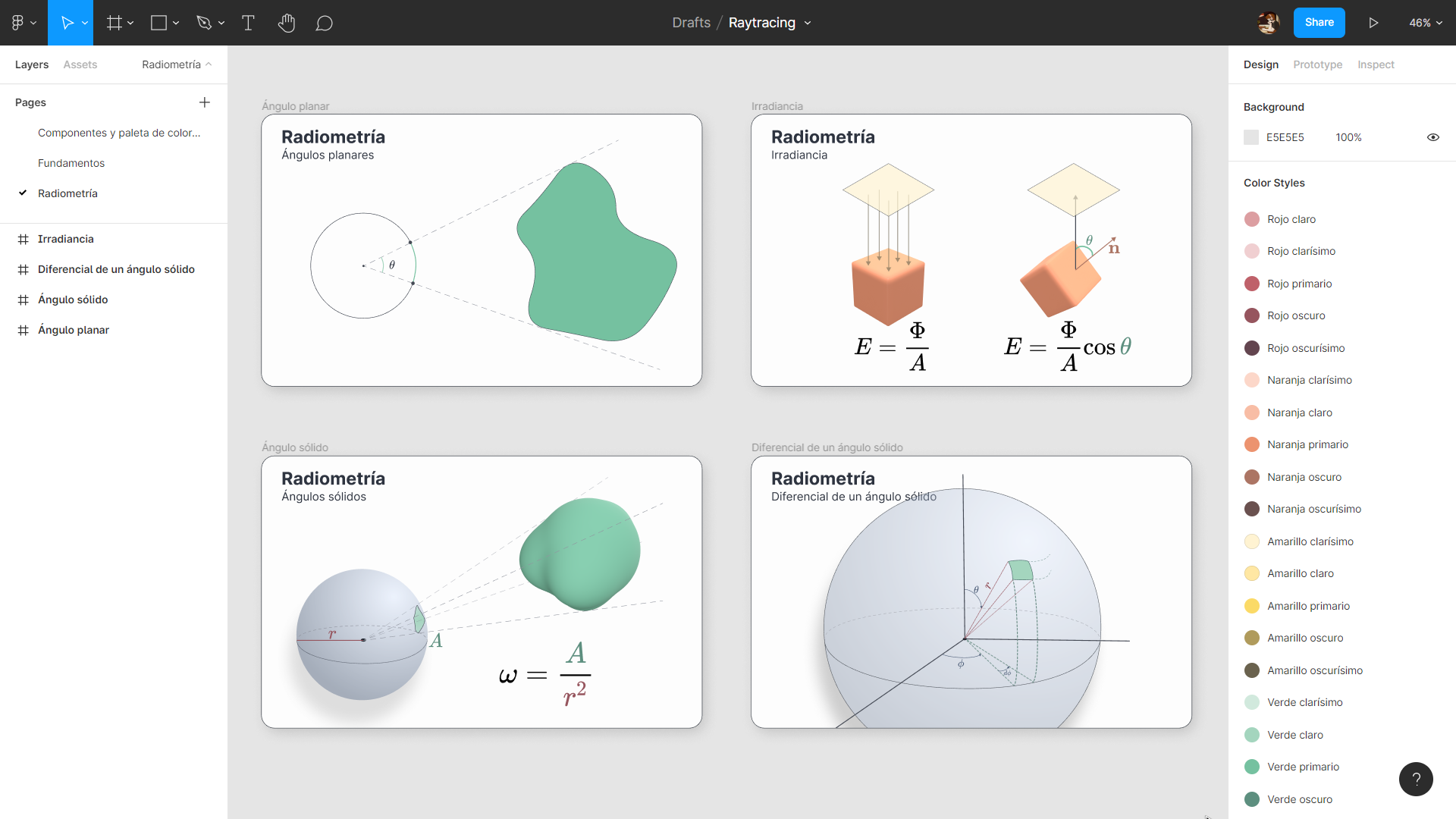
Una de las características más útiles es poder exportar rápidamente la imagen. Esto permite hacer cambios rápidos y registrarlos en el repositorio fácilmente. Además, permite instalar plugins. Uno de ellos ha resultado especialmente útil: Latex Complete (Krieger 2022). Esto nos permite incrustar código LaTeX en el documento en forma de SVG.
Como es normal, hay muchos otros programas que han intervenido en el desarrollo. Estos son algunos de ellos:
La página Github (Github
2022) ha alojado prácticamente todo el contenido del trabajo;
desde el programa, hasta la documentación online. El repositorio se
puede consultar en github.com/Asmilex/Raytracing (Millán
2022b).
Se ha escogido Github en vez de sus competidores (como Gitlab o Bitbucket) por los siguientes motivos:
Entremos en detalle en algunos de los puntos anteriores:
Cuando hablamos de integración continua, nos referimos a ciertos programas que corren en un repositorio y se encargan de hacer ciertas transformaciones al código, de forma que este se prepare para su presentación final. En esencia, automatizan algunas tareas habituales de un desarrollo de software. (Merelo 2021)
En este trabajo lo usaremos para compilar la documentación. De esta forma, no necesitamos lidiar con “proyecto final”, “proyecto final definitivo”, “proyecto final final v2”, etc. Simplemente, cuando registremos un cambio en los ficheros Markdown (lo que se conoce en git como un commit), y lo subamos a Github (acción de push), se ejecutará un denominado action que operará sobre nuestros archivos.
Tendremos dos tipos de Actions: uno que se encarga de compilar la web, y otro el PDF. En esencia, operan de la siguiente manera:
.md en el
último commit subido. Si no es el caso, para.pandoc.
docs/index.html. Publica la web a
Github Pages.docs/TFG.pdf
El workflow de la web corre automáticamente, mientras que para generar el PDF hace falta activación manual. Aunque no es del todo correcto almacenar ficheros binarios en un repositorio de git, no me resulta molesto personalmente. Así que, cuando considero que es el momento oportuno, lo hago manualmente. Además, también se activa por cada release que se crea.
Volviendo a la web, Github permite alojar páginas web para un
repositorio. Activando el parámetro correcto en las opciones del
repositorio, y configurándolo debidamente, conseguimos que lea el
archivo index.html generado por el Action y lo despliegue.
Esto es potentísimo: con solo editar una línea de código y subir los
cambios, conseguimos que la web se actualice al instante.
Para generar los archivos nos hace falta una distribución de LaTeX,
Pandoc, y todas las dependencias (como filtros). Como no encontré ningún
contenedor que sirviera mi propósito, decidí crear uno. Se encuentra en
el repositorio de Dockerhub (Millán
2022a). Esta imagen está basada en
dockershelf/latex:full (Dockershelf 2022). Por desgracia, es
muy pesada para ser un contenedor. Desafortunadamente, una
instalación de LaTeX ocupa una cantidad de espacio considerable; y para
compilar el PDF necesitamos una muy completa, por lo que debemos lidiar
con este overhead. Puedes encontrar el Dockerfile en
./Dockerfile.
Las tareas pendientes se gestionan mediante issues. Cada vez que se tenga un objetivo particular para el desarrollo, se anota un issue. Cuando se genere un commit que avance dicha tarea, se etiqueta con el número correspondiente al issue. De esta forma, todas las confirmaciones relacionadas con la tarea quedan recogidas en la página web.
Esto permite una gestión muy eficiente de los principales problemas y objetivos pendientes de la aplicación.
Los issues se agrupan en milestones, o productos mínimamente viables. Estos issues suelen estar relacionados con algún apartado importante del desarrollo.
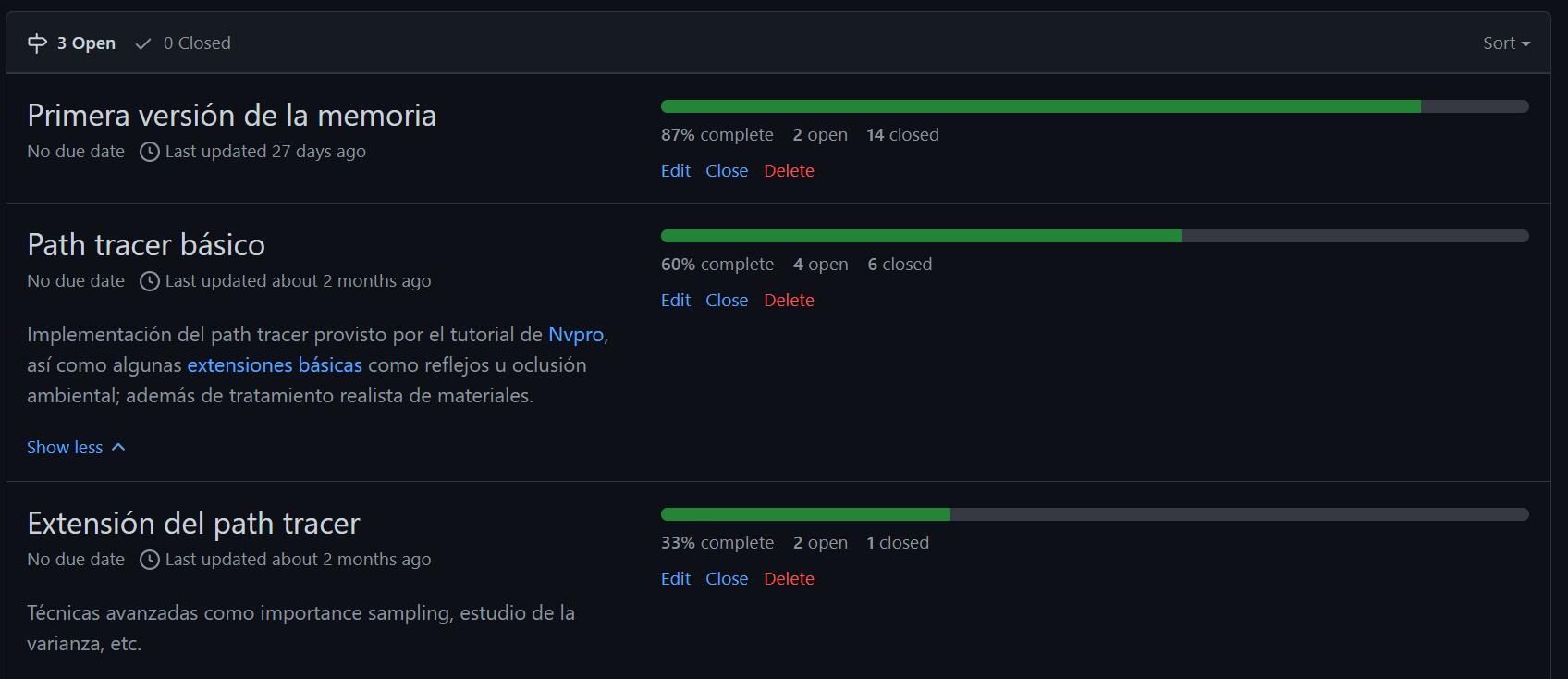
De esta forma, podemos ver todo lo que queda pendiente para la fecha de entrega.
Para añadir mayor granularidad a la gestión de tareas y proporcionar una vista informativa, se utiliza Github Projects. En esencia, esta aplicación es un acompañante del repositorio estilo Asana.
Una de las alternativas que se planteó al inicio fue Linear (Linear 2022), una aplicación de gestión de issues similar a Projects. Sin embargo, la conveniencia de tener Projects integrado en Github supuso un punto a favor para este gestor. De todas formas, el equipo de desarrollo se compone de una persona, así que no hace falta complicar excesivamente el workflow.
El desarrollo general de la documentación no ha seguido este sistema
de issues, pues está sujeta a cambios constantes y cada
commit está marcado con [:notebook:]. No obstante,
ciertos problemas relacionados con ella, como puede ser el formato de
entrega, sí que quedan recogidos como un issue.
Finalmente, cuando se produce un cambio significativo en la
aplicación (como puede ser una refactorización, una implementación
considerablemente más compleja…) se genera una nueva rama. Cuando se ha
cumplido el objetivo, se mergea la rama con la principal
main mediante un pull request. Esto proporciona un
mecanismo de robustez ante cambios complejos.
Una de los detalles que has podido apreciar si has entrado al repositorio es un estilo de commit un tanto inusual. Aunque parece un detalle de lo más insustancial, añadir emojis a los mensajes de commits añade un toque particular al repositorio, y permite identificar rápidamente el tipo de cambio.
Cada uno tiene un significado particular. En esta tabla se recogen sus significados:
It’s dangerous to go alone, take this.
Tener en mente todos los conceptos y sus expresiones que aparecen en un libro como este es prácticamente imposible. Tampoco hay necesidad de ello, realmente. ¡Vaya desperdicio de cabeza! Por eso, aquí tienes recopilada una lista con todos los elementos importantes y un enlace a sus secciones correspondientes.
| Concepto | Notación |
|---|---|
| Escalares | Letras minúsculas. Generalmente, \(a, b, c, k, \dots\) |
| Puntos | Letras minúsculas en negrita. Generalmente, \(\mathbf{p}, \mathbf{q}, \dots\) |
| Vectores | Letras minúsculas en negrita: \(\mathbf{v, w, n}, \dots\). |
| Matrices | Letras mayúsculas en negrita: \(\mathbf{M}\). Por columnas. |
| Producto escalar | \(\mathbf{v} \cdot \mathbf{w}\). Si es el producto escalar de un vector consigo mismo, a veces pondremos \(\mathbf{v}^2\) |
| Producto vectorial | \(\mathbf{v} \times \mathbf{w}\) |
| Concepto | Expresiones y comentarios |
|---|---|
| Rayo | \(P(t) = o + td\) |
| Ray casting | Disparar un rayo hacia la escena virtual, de forma que impacta con alguna superficie. |
| Normal en un punto | Vector perpendicular a cualquier punto de la superficie: \(\mathbf{n} = \nabla F(P) = \left( \frac{\partial F(P)}{\partial x}, \frac{\partial F(P)}{\partial y}, \frac{\partial F(P)}{\partial z}\right )\) |
| Concepto | Expresiones y comentarios |
|---|---|
| Carga de energía | Energía de un fotón. \(Q = hf = \frac{hc}{\lambda}\) |
| Flujo radiante o potencia | Tasa de producción de energía de una
fuente de luz. \(\begin{aligned}& \Phi = \frac{dQ}{dt} \\ & \Phi = \int_{A}\int_{H^2(\mathbf{n})}{L_o(p, \omega) d\omega^\bot dA}\end{aligned}\) |
| Irradiancia o radiancia emitida | Flujo radiente que recibe una superficie.
\(\begin{aligned} & E = \frac{\Phi}{A} \\ & E(p) = \frac{d\Phi}{dA} \\ & E(p, \mathbf{n}) = \int_{\Omega}{L_i(p, \omega) \left\lvert cos\theta \right\rvert d\omega} \\ & E(p, \mathbf{n}) = \int_{0}^{2\pi}\int_{0}^{\pi/2}{L_i(p, \theta, \phi) \cos\theta\ \sin\theta\ d\theta\ d\phi} \\ & E(p, \mathbf{n}) = \int_{A}{L\cos\theta\ \frac{\cos\theta_o}{r^2}dA} \end{aligned}\) |
| Ángulo sólido, derivada [11] [16] | Medida del campo de visión de un objeto
desde un cierto punto. \(\sigma = \frac{A}{r^2}\) \(d\sigma = \sin\theta\ d\theta\ d\phi\) \(d\sigma = \frac{dA\cos\theta}{r^2}\) |
| Coordenadas esféricas | Sistema de coordenadas \((r, \theta, \phi)\) usado habitualmente
para describir posiciones en una esfera. \(x = \sin\theta\cos\phi,\ y = \sin\theta\sin\phi,\ z = \cos\theta\) |
| Intensidad radiante | Densidad angular de flujo radiante. \(I = \frac{d\Phi}{d\omega}\) |
| Radiancia | Flujo radiante emitido en un cierto cono
de direcciones. \(\begin{aligned} & L(p, \omega) = \frac{dE_\omega(p)}{d\omega} \\ & L(p, \omega) = \frac{d^2\Phi(p, \omega)}{d\omega\ dA^\bot} = \frac{d^2\Phi(p, \omega)}{d\omega\ dA\ \cos\theta}\end{aligned}\) |
| Radiancia incidente | Radiancia que recibe una superficie desde
la dirección \(\omega\). \(\begin{aligned} L_i(p, \omega) \end{aligned}\) |
| Radiancia reflejada o de salida | Radiancia que emite una superficie hacia
una dirección \(\omega\). \(\begin{aligned} L_o(p, \omega) \end{aligned}\) |
| BRDF | Cómo se dispersa la luz cuando impacta una
superficie dependiendo de la dirección. \(\begin{aligned}& f_r(p, \omega_o \leftarrow \omega_i) = \frac{dL_o(p, \omega_o)}{dE(p, \omega_i)} = \frac{dL_o(p, \omega_o)}{L_i(p, \omega_i) \cos\theta_i\ d\omega_i}\end{aligned}\) |
| BTDF | Cómo se transmite la luz cuando impacta
una superficie dependiendo de la dirección. \(f_t(p, \omega_o \leftarrow \omega_i)\) |
| BSDF | Combinación de la BRDF y la BTDF. \(f(p, \omega_o \leftarrow \omega_i)\) |
| Hemisferio de direcciones alrededor de un vector | \(H^2(\mathbf{n})\) |
| Albedo o reflectancia hemisférica | Proporción de luz reflejada por una
superficie. \(\rho_{hd}(\omega_o) = \int_{H^2(n)}{f_r(p, \omega_o \leftarrow \omega_i) \left\lvert \cos\theta_i \right\rvert\ d\omega_i}\) |
| Tipos de materiales | Difusos, especulares brillantes, especulares perfectos, retrorreflectores |
| Reflexión | Efecto de la luz cuando impacta un espejo.
\(\mathbf{r} = \mathbf{i} - 2 (\mathbf{i} \cdot \mathbf{n}) \mathbf{n}\) |
| Ley de Snell | Relación entre los ángulos de un rayo al
cambiar de medio. \(\eta_1 \sin\theta_1 = \eta_2 \sin\theta_2\) |
| Aproximación de Schlick | Simplificación de las ecuaciones de
Fresnel. \(R(\theta_1) = R_0 + (1 - R_0)(1 - \cos\theta_1)^5\) |
| Ecuación de dispersión | Ecuación para la radiancia emitida hacia
una dirección en un cierto punto. \(\begin{aligned}L_o(p, \omega_o) = \int_{\mathbb{S}^2}{f(p, \omega_o \leftarrow \omega_i)L_i(p, \omega_i)\left\lvert \cos\theta_i \right\rvert d\omega_i}\end{aligned}\) |
| Radiancia reflejada | Radiancia reflejada hacia una dirección en
un cierto punto. \(\begin{aligned}L_r(p, \omega_o) = \int_{H^2(\mathbf{n})}{f(p, \omega_o \leftarrow \omega_i) L_i(p, \omega_i) \cos\theta_i\ d\omega_i}\end{aligned}\) |
| Rendering equation o ecuación del transporte de luz | La ecuación más importante de la
informática gráfica. Describe analíticamente la cantidad de luz de un
punto en función de su entorno. \(\begin{aligned}L_o(p, \omega_o) = L_e(p, \omega_o) + \int_{H^2(\mathbf{n})}{f(p, \omega_o \leftarrow \omega_i) L_i(p, \omega_i) \cos\theta_i\ d\omega_i} \end{aligned}\) |
| Concepto | Expresiones |
|---|---|
| Variable aleatoria | Regla que asigna un valor numérico a cada
caso de un proceso de azar. Usualmente, \(X, Y, \xi\)… |
| Función masa de probabilidad (discretas) o de densidad (continuas) | Función que permite conocer la
probabilidad de un suceso. Discretas: \(P\left[ X \in \text{Conjunto} \right]\) Continuas: \(f_X, p_X\) |
| Función de distribución | Probabilidad de que una variable aleatoria
se quede por debajo de un cierto valor. \(F_X(x) = P\left[ X \le x \right]\) |
| Esperanza | Generalización de la media ponderada para
una cierta variable aleatoria. \(E\left[ X \right]\) |
| Varianza | Medida de la dispersión de la distribución
de una variable aleatoria. \(Var\left[ X \right]\) |
| Estimador | Función de la muestra de una variable
aleatoria que toma valores en el conjunto de parámetros de una
distribución. \(T(X_1, \dots, X_n) = \theta \in \Theta\) |
| Estimador de Monte Carlo | Estimador cuya esperanza es la media de
una variable aleatoria. \(\hat\mu_N = \frac{1}{N} \sum_{i = 1}^{N}{Y_i}\) \(\Rightarrow E\left[ \hat\mu_N \right] = \mu\) |
| Estimador de Monte Carlo (para una integral) | Estimador de Monte Carlo que permite
conocer el valor de una integral \(\int_S f(x)
p_X(x) dx\) a partir de muestras de una variable aleatoria \(X \sim p_X\) Simple: \(\hat{I}_N = \frac{1}{N} \sum_{i = 1}^{N}{f(X_i)}\) Por importancia: \(\tilde{I}_N = \frac{1}{N} \sum_{i=1}^N{\frac{f(X_i)p_X(X_i)}{q_X(X_i)}}, \quad X_i \sim q_X\) Transporte de luz: \(\tilde{I}_N = \frac{1}{N} \sum_{i=1}^N{\frac{f(X_i)}{p_X(X_i)}}\) |
| Orden de convergencia del estimador de Monte Carlo | \(\mathcal{O}(N^{-1/2})\) |
| Concepto | Expresiones |
|---|---|
| Rasterización | Técnica de producción de imágenes por ordenador en la que la geometría virtual es proyectada en un plano 2D. |
| Ray tracing | Algoritmo basado en la generación de rayos de luz que permite generar imágenes más realistas que en rasterización |
| Path tracing | Algoritmo basado en ray tracing en el que se simulan múltiples caminos de luz. |
| Ecuación del transporte de luz estimada por Monte Carlo | \(\begin{aligned}\frac{1}{N} \sum_{j = 1}^{N}{\frac{f(p, \omega_o \leftarrow \omega_j) L_i(p, \omega_j) \cos\theta_j}{P\left[ \omega_j \right]}}\end{aligned}\) |
| Rendering engine o motor | Software diseñado para producir imágenes de entornos virtuales utilizando hardware específico. |
| GPU (Graphics Processing Unit) | Tarjeta gráfica; dispositivo especializado en la aceleración de cálculos necesarios en la producción de imágenes. |
| Graphic API | Interaz de programación de aplicaciones para la creación de imágenes por ordenador. |
| Vulkan | API gráfica de código abierto desarrollada por Khonos. |
| Estructura de aceleración | Forma de representar la geometría de una escena de manera que se optimicen las intersecciones de objetos y rayos |
| Bounding Volume Hierarchy (BVH) | Tipo de estructura de aceleración basada en cajas delimitantes (bounding boxes) |
| Axis-Aligned Bounding Box (AABB) | Tipo de BVH alineada con los ejes virtuales. |
| Bottom-Level Acceleration Structure (BLAS) | Estructura utilizada por Vulkan para almacenar la geometría de un objeto individual. |
| Top-Level Acceleration Structure (TLAS) | Estructura utilizada por Vulkan para guardar la información de las instancias de un objeto. |
| Shader | Programa que se ejecuta en una tarjeta gráfica. |
| Ray generation shader | Shader que se encarga de la generación inicial de rayos. |
| Closest hit shader | Shader que se ejecuta para el primer impacto de un rayo con una geometría válida. |
| Any-hit shader | Similar al closest hit. Shader que corre en cada intersección. |
| Miss shader | Shader que se ejecuta cuando no se impacta ninguna geometría. |
| Intersection shader | Shader que se encarga de computar intersecciones con objetos. |
| Shader Binding Table (SBT) | Estructura específica de ray tracing que permite guardar referencias a shaders y sus parámetros para ser ejecutadas cuando se impacte una geometría específica. |
| Push constant | Estructura que almacena elementos constantes comunes para todos los tipos de shaders. |
| Payload | Estructura que permite traspasar información variable entre diferentes shaders. |
| Wavefront | Formato de archivo que permite abstraer objetos virtuales y sus tipos de materiales. |
| Antialiasing | Técnica para suavizar los dientes de sierra generados por líneas diagonales. |
| Corrección de gamma | Operación utilizada en fotografía para corregir la luminancia con el fin de compensar la percepción no lineal del brillo por parte de los humanos. |
| Concepto | Expresiones |
|---|---|
| Frame time | Tiempo que tarda un motor en renderizar una imagen. Medido en milisegundos. |
| Frame rate | Tasa de imágenes por segundo (FPS, frames per second) que es capaz de producir un motor. Es la inversa del frame time. |
| Iluminación global | Fenómeno físico producido por el rebote constante de fotones en un entorno. Es difícil simular sin path tracing. |
No entraremos en detalle sobre la naturaleza de la luz. Sin embargo, si te pica la curiosidad, hay muchos divulgadores como (Crespo 2021) que han tratado el tema con suficiente profundidad.↩︎
Recuerda que estamos omitiendo la longitud de onda \(\lambda\).↩︎
En su defecto, si tenemos una función de densidad \(p_X\), podemos hallar la función de distribución haciendo \(F_X(x) = P[X < x] = \int_{x_{min}}^{x}{p_X(t)dt}\).↩︎
No tiene por qué ser en tiempo, pero generalmente se considera este tipo de variable.↩︎
Esto no es del todo cierto. Aunque generalmente suelen ser excepciones debido al coste computacional de RT en tiempo real, existen algunas implementaciones que son capaces de correrlo por software. Notablemente, el motor de Crytek, CryEngine, es capaz de mover ray tracing basado en hardware y en software (Crytek 2020)↩︎
Afortunadamente, esto tampoco es completamente cierto. La compañía desarrolladora y distribuidora de videojuegos Valve Corporation (Valve Software 2022b) ha creado una pieza de software fascinante: Proton (Valve Software 2022a). Proton utiliza Wine para emular software en Linux que solo puede correr en plataformas Windows. La versión 2.5 añadió soporte para traducción de bindings de DXR a KHR, lo que permite utilizar DirectX12 ray tracing en sistemas basados en Linux. El motivo de este software es expandir el mercado de videojuegos disponibles en su consola, la Steam Deck.↩︎
A no ser que se utilicen motion vectors, los cuales codifican información sobre el movimiento de un objeto al pasar de un frame a otro. Estos permiten implementar técnicas como temporal antialiasing, los cuales veremos en una sección posterior.↩︎